Zum Inhalt springen

Lösung Eigenschaften und Nullstellen

Version 4.1 von Holger Engels am 2025/03/11 11:59

Gegeben ist die Funktion:

\[i(x) = (x+2)e^{-x}\]

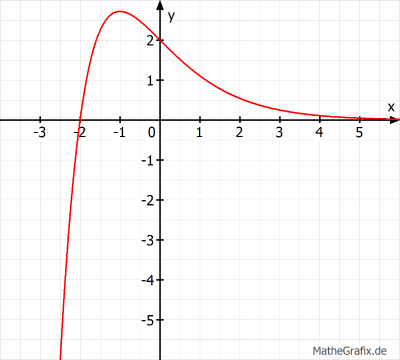
Eigenschaften und Nullstellen.png

  1. Bestimme den Schnittpunkt mit der y-Achse.
    \(i(0) = (0+2)e^{-0} = 2 \Rightarrow S_y(0|2)\)

  2. Berechne die Nullstelle.
    \(i(x) = 0 \Rightarrow (x+2)e^{-x} = 0 \quad || SVNP\)
    \(\Rightarrow (x+2) = 0 \wedge e^{-x} = 0 \quad || e^{-x} \neq 0\)
    \(\Rightarrow x = -2\)

  3. Beschreibe das globale Verhalten und gib die Gleichung der Asymptoten an.