BPE 4.4 Aufstellen von Funktionstermen
K4 Ich kann den passenden Ansatz für die Ermittlung eines Funktionsterms anhand gegebener Bedingungen bestimmen
K4 K5 Ich kann den Funktionsterm anhand verbal gegebener Bedingungen aufstellen
K4 K5 Ich kann den Funktionsterm anhand tabellarisch gegebener Bedingungen aufstellen
K4 K5 Ich kann den Funktionsterm anhand eines Schaubilds aufstellen
1 Graph durch Punkte (8 min) 𝕃
Begründe, ob folgende Aussagen über das Schaubild der Funktion \(f(x)=\frac{2}{3}\cdot e^x+4\) wahr oder falsch sind.
- Das Schaubild schneidet die y-Achse bei \(y=4\).
- Das Schaubild besitzt eine Nullstelle.
- Der Graph nähert sich für \(x \to -\infty \) ihrer Asymptote an.
- Es ist: \(f(1)=4+\frac{2e}{3}\)
| AFB I - K1 K6 | Quelle Frauke Beckstette, Simone Kanzler |
2 Graph durch Punkte (8 min) 𝕃
Bestimme den Funktionsterm der Exponantialfunktion
- \(f_1(x)=q^x\), deren Schaubild durch den Punkt \(P(5|243)\) verläuft.
- \(f_2(x)=q^x\), deren Schaubild durch den Punkt \(Q(-1|1,5)\) verläuft.
- \(f_3(x)=a\cdot q^x\), deren Schaubild durch die Punkte \(A(0|-2)\) und \(B(3|-6,75)\) verläuft.
| AFB II - K5 | Quelle Frauke Beckstette |
3 Vom Bild zum Funktionsterm (6 min) 𝕃
Die Schaubilder gehören zu einer Exponentialfunktion der Form \(f(x)=ae^bx+d\).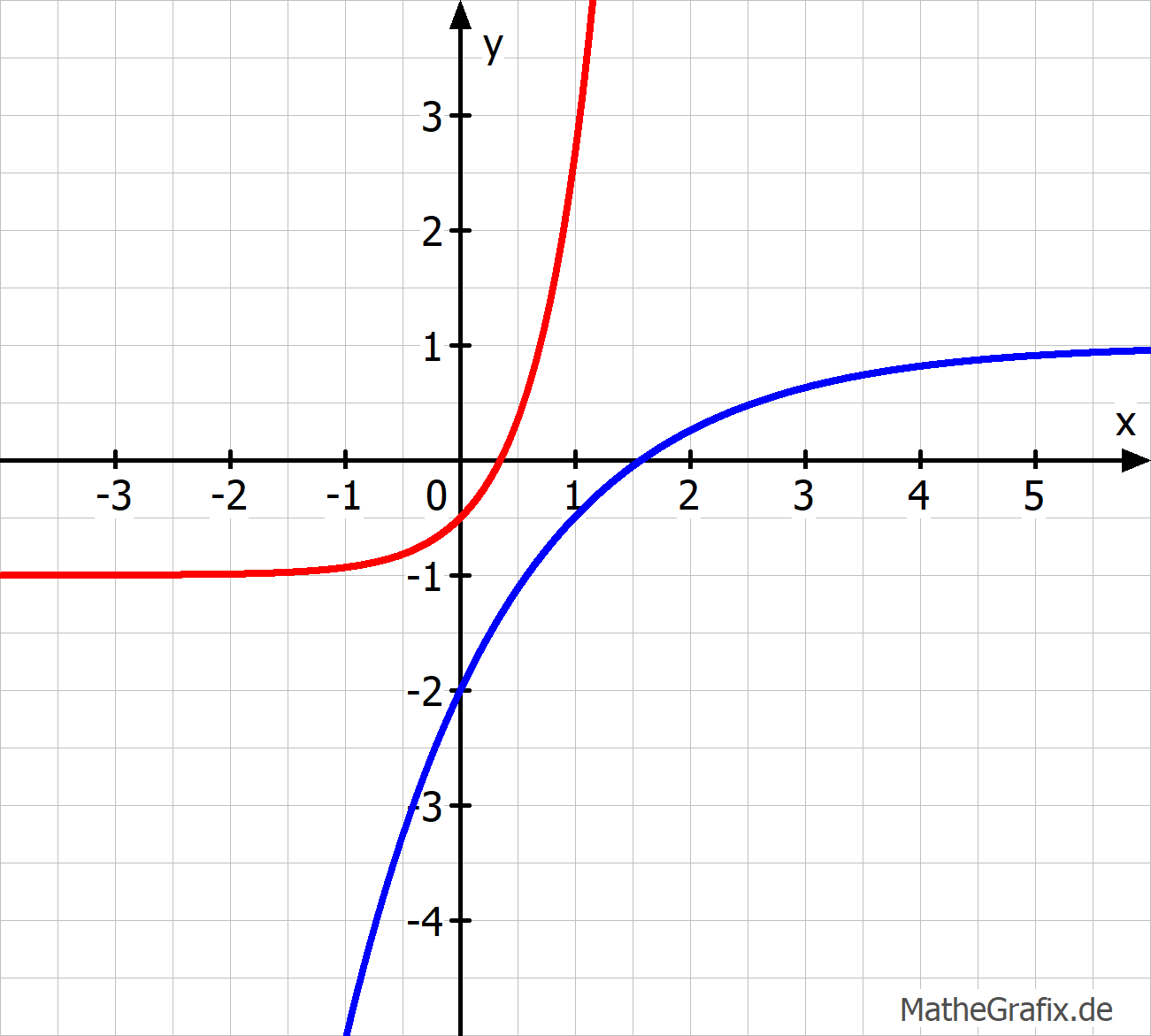
Bestimme jeweils die Werte der Parameter \(a\), \(b\) und \(d\).
Gib den Funktionsterm an.
| AFB II - K4 K5 | Quelle Frauke Beckstette, Simone Kanzler |
4 Vom Text zum Funktionsterm (3 min) 𝕃
Das Schaubild einer Exponentialfunktion der Form \(f(x)=aq^x+d\) hat die Asymptote mit der Gleichung \(y=-1,7\), schneidet die \(x-\)Achse bei \(x=2,5\) und die \(y-\)Achse in \(S_y(0|-1,4)\).
Bestimme den Funktionsterm.
| AFB II - K4 K5 | Quelle Frauke Beckstette, Simone Kanzler |
5 Von der Tabelle zum Funktionsterm (8 min) 𝕃
Die dargestellte Wertetabelle gehört zu einer Exponentialfunktion.

Bestimme einen passenden Funktionsterm.
| AFB III - K3 K4 K5 | Quelle Frauke Beckstette, Simone Kanzler |
