Mittlere und momentane Änderungsrate
Die Schülerinnen und Schüler erläutern in verschiedenen Anwendungssituationen den Unterschied zwischen momentaner und durchschnittlicher Änderungsrate und deuten grafisch oder rechnerisch ermittelte Änderungsraten im Anwendungskontext.
Mittlere Änderungsrate
Das Makro [aufgabe] konnte nicht ausgeführt werden. Grund: [Parameter [afb] is mandatory]. Klicke auf diese Nachricht, um Details zu erfahren.
org.xwiki.rendering.macro.parameter.MacroParameterException: Parameter [afb] is mandatory
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.validate(DefaultWikiMacro.java:222)
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.execute(DefaultWikiMacro.java:121)
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.execute(DefaultWikiMacro.java:61)
at org.xwiki.rendering.internal.transformation.macro.MacroTransformation.transform(MacroTransformation.java:441)
at org.xwiki.rendering.internal.transformation.DefaultRenderingContext.transformInContext(DefaultRenderingContext.java:183)
at org.xwiki.rendering.internal.transformation.DefaultTransformationManager.performTransformations(DefaultTransformationManager.java:88)
at org.xwiki.rendering.internal.transformation.XWikiTransformationManager.superPerformTransformations(XWikiTransformationManager.java:95)
at org.xwiki.rendering.internal.transformation.XWikiTransformationManager.performTransformations(XWikiTransformationManager.java:88)
at org.xwiki.display.internal.DocumentContentAsyncExecutor.executeInCurrentExecutionContext(DocumentContentAsyncExecutor.java:397)
at org.xwiki.display.internal.DocumentContentAsyncExecutor.execute(DocumentContentAsyncExecutor.java:269)
at org.xwiki.display.internal.DocumentContentAsyncRenderer.execute(DocumentContentAsyncRenderer.java:112)
at org.xwiki.rendering.async.internal.block.AbstractBlockAsyncRenderer.render(AbstractBlockAsyncRenderer.java:157)
at org.xwiki.rendering.async.internal.block.AbstractBlockAsyncRenderer.render(AbstractBlockAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:290)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.execute(DefaultBlockAsyncRendererExecutor.java:125)
at org.xwiki.display.internal.DocumentContentDisplayer.display(DocumentContentDisplayer.java:93)
at org.xwiki.display.internal.DocumentContentDisplayer.display(DocumentContentDisplayer.java:46)
at org.xwiki.display.internal.DefaultDocumentDisplayer.display(DefaultDocumentDisplayer.java:96)
at org.xwiki.display.internal.DefaultDocumentDisplayer.display(DefaultDocumentDisplayer.java:39)
at org.xwiki.sheet.internal.SheetDocumentDisplayer.display(SheetDocumentDisplayer.java:123)
at org.xwiki.sheet.internal.SheetDocumentDisplayer.display(SheetDocumentDisplayer.java:52)
at org.xwiki.display.internal.ConfiguredDocumentDisplayer.display(ConfiguredDocumentDisplayer.java:68)
at org.xwiki.display.internal.ConfiguredDocumentDisplayer.display(ConfiguredDocumentDisplayer.java:42)
at com.xpn.xwiki.doc.XWikiDocument.display(XWikiDocument.java:1433)
at com.xpn.xwiki.doc.XWikiDocument.getRenderedContent(XWikiDocument.java:1569)
at com.xpn.xwiki.doc.XWikiDocument.displayDocument(XWikiDocument.java:1519)
at com.xpn.xwiki.doc.XWikiDocument.displayDocument(XWikiDocument.java:1488)
at com.xpn.xwiki.api.Document.displayDocument(Document.java:822)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.value(ASTReference.java:704)
at org.apache.velocity.runtime.parser.node.ASTExpression.value(ASTExpression.java:75)
at org.apache.velocity.runtime.parser.node.ASTSetDirective.render(ASTSetDirective.java:242)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:190)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.xwiki.velocity.internal.directive.TryCatchDirective.render(TryCatchDirective.java:86)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:856)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:811)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:803)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:79)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:73)
at org.xwiki.template.script.TemplateScriptService.render(TemplateScriptService.java:54)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.render(ASTReference.java:492)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.directive.VelocimacroProxy.render(VelocimacroProxy.java:217)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:331)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:261)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:856)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:811)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:803)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:79)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:73)
at org.xwiki.template.script.TemplateScriptService.render(TemplateScriptService.java:54)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.render(ASTReference.java:492)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.directive.VelocimacroProxy.render(VelocimacroProxy.java:217)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:331)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:261)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:171)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:190)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:849)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:835)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.render(DefaultTemplateManager.java:91)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.render(DefaultTemplateManager.java:85)
at com.xpn.xwiki.XWiki.evaluateTemplate(XWiki.java:2555)
at com.xpn.xwiki.web.Utils.parseTemplate(Utils.java:180)
at com.xpn.xwiki.web.XWikiAction.execute(XWikiAction.java:651)
at com.xpn.xwiki.web.XWikiAction.execute(XWikiAction.java:339)
at com.xpn.xwiki.web.LegacyActionServlet.service(LegacyActionServlet.java:111)
at jakarta.servlet.http.HttpServlet.service(HttpServlet.java:723)
at org.eclipse.jetty.ee11.servlet.ServletHolder$NotAsync.service(ServletHolder.java:1393)
at org.eclipse.jetty.ee11.servlet.ServletHolder.handle(ServletHolder.java:750)
at org.eclipse.jetty.ee11.servlet.ServletHandler$ChainEnd.doFilter(ServletHandler.java:1668)
at com.xpn.xwiki.web.ActionFilter.doFilter(ActionFilter.java:123)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.wysiwyg.filter.ConversionFilter.doFilter(ConversionFilter.java:71)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SetHTTPHeaderFilter.doFilter(SetHTTPHeaderFilter.java:66)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.resource.servlet.RoutingFilter.doFilter(RoutingFilter.java:135)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SavedRequestRestorerFilter.doFilter(SavedRequestRestorerFilter.java:212)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SafeRedirectFilter.doFilter(SafeRedirectFilter.java:106)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.ResolveRelativeRedirectFilter.doFilter(ResolveRelativeRedirectFilter.java:129)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SourceURLResolverFilter.doFilter(SourceURLResolverFilter.java:177)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SetCharacterEncodingFilter.doFilter(SetCharacterEncodingFilter.java:120)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:208)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.eclipse.jetty.ee11.websocket.servlet.WebSocketUpgradeFilter.doFilter(WebSocketUpgradeFilter.java:199)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.eclipse.jetty.ee11.servlet.ServletHandler$MappedServlet.handle(ServletHandler.java:1602)
at org.eclipse.jetty.ee11.servlet.ServletChannel.dispatch(ServletChannel.java:868)
at org.eclipse.jetty.ee11.servlet.ServletChannel.handle(ServletChannel.java:449)
at org.eclipse.jetty.ee11.servlet.ServletHandler.handle(ServletHandler.java:470)
at org.eclipse.jetty.security.SecurityHandler.handle(SecurityHandler.java:546)
at org.eclipse.jetty.ee11.servlet.SessionHandler.handle(SessionHandler.java:763)
at org.eclipse.jetty.server.handler.ContextHandler.handle(ContextHandler.java:1224)
at org.eclipse.jetty.server.handler.ContextHandlerCollection.handle(ContextHandlerCollection.java:178)
at org.eclipse.jetty.server.Server.handle(Server.java:197)
at org.eclipse.jetty.server.internal.HttpChannelState$HandlerInvoker.run(HttpChannelState.java:787)
at org.eclipse.jetty.server.internal.HttpConnection.onFillable(HttpConnection.java:410)
at org.eclipse.jetty.server.internal.HttpConnection$FillableCallback.succeeded(HttpConnection.java:1805)
at org.eclipse.jetty.io.FillInterest.fillable(FillInterest.java:105)
at org.eclipse.jetty.io.SelectableChannelEndPoint$1.run(SelectableChannelEndPoint.java:54)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.runTask(AdaptiveExecutionStrategy.java:492)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.epcRunTask(AdaptiveExecutionStrategy.java:428)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.consumeTask(AdaptiveExecutionStrategy.java:401)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.tryProduce(AdaptiveExecutionStrategy.java:255)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.run(AdaptiveExecutionStrategy.java:204)
at org.eclipse.jetty.util.thread.ReservedThreadExecutor$ReservedThread.run(ReservedThreadExecutor.java:317)
at org.eclipse.jetty.util.thread.QueuedThreadPool.runJob(QueuedThreadPool.java:1009)
at org.eclipse.jetty.util.thread.QueuedThreadPool$Runner.doRunJob(QueuedThreadPool.java:1239)
at org.eclipse.jetty.util.thread.QueuedThreadPool$Runner.run(QueuedThreadPool.java:1194)
at java.base/java.lang.Thread.run(Thread.java:1583)
Berechnen Sie die durchschnittliche Änderungsrate der Funktion f im Intervall \(\left[-3;2\right]\).
a) \(f(x)=5x^2-3\)
b) \(g(x)=-x^3+2x^2\)
Unbekanntes Makro: tags. Klicke auf diese Nachricht, um Details zu erfahren.
Das Makro [tags] befindet sich nicht in der Liste der registrierten Makros. Überprüfen Sie die Schreibweise oder wenden Sie sich an Ihren Administrator.
Das Makro [aufgabe] konnte nicht ausgeführt werden. Grund: [Parameter [afb] is mandatory]. Klicke auf diese Nachricht, um Details zu erfahren.
org.xwiki.rendering.macro.parameter.MacroParameterException: Parameter [afb] is mandatory
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.validate(DefaultWikiMacro.java:222)
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.execute(DefaultWikiMacro.java:121)
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.execute(DefaultWikiMacro.java:61)
at org.xwiki.rendering.internal.transformation.macro.MacroTransformation.transform(MacroTransformation.java:441)
at org.xwiki.rendering.internal.transformation.DefaultRenderingContext.transformInContext(DefaultRenderingContext.java:183)
at org.xwiki.rendering.internal.transformation.DefaultTransformationManager.performTransformations(DefaultTransformationManager.java:88)
at org.xwiki.rendering.internal.transformation.XWikiTransformationManager.superPerformTransformations(XWikiTransformationManager.java:95)
at org.xwiki.rendering.internal.transformation.XWikiTransformationManager.performTransformations(XWikiTransformationManager.java:88)
at org.xwiki.display.internal.DocumentContentAsyncExecutor.executeInCurrentExecutionContext(DocumentContentAsyncExecutor.java:397)
at org.xwiki.display.internal.DocumentContentAsyncExecutor.execute(DocumentContentAsyncExecutor.java:269)
at org.xwiki.display.internal.DocumentContentAsyncRenderer.execute(DocumentContentAsyncRenderer.java:112)
at org.xwiki.rendering.async.internal.block.AbstractBlockAsyncRenderer.render(AbstractBlockAsyncRenderer.java:157)
at org.xwiki.rendering.async.internal.block.AbstractBlockAsyncRenderer.render(AbstractBlockAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:290)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.execute(DefaultBlockAsyncRendererExecutor.java:125)
at org.xwiki.display.internal.DocumentContentDisplayer.display(DocumentContentDisplayer.java:93)
at org.xwiki.display.internal.DocumentContentDisplayer.display(DocumentContentDisplayer.java:46)
at org.xwiki.display.internal.DefaultDocumentDisplayer.display(DefaultDocumentDisplayer.java:96)
at org.xwiki.display.internal.DefaultDocumentDisplayer.display(DefaultDocumentDisplayer.java:39)
at org.xwiki.sheet.internal.SheetDocumentDisplayer.display(SheetDocumentDisplayer.java:123)
at org.xwiki.sheet.internal.SheetDocumentDisplayer.display(SheetDocumentDisplayer.java:52)
at org.xwiki.display.internal.ConfiguredDocumentDisplayer.display(ConfiguredDocumentDisplayer.java:68)
at org.xwiki.display.internal.ConfiguredDocumentDisplayer.display(ConfiguredDocumentDisplayer.java:42)
at com.xpn.xwiki.doc.XWikiDocument.display(XWikiDocument.java:1433)
at com.xpn.xwiki.doc.XWikiDocument.getRenderedContent(XWikiDocument.java:1569)
at com.xpn.xwiki.doc.XWikiDocument.displayDocument(XWikiDocument.java:1519)
at com.xpn.xwiki.doc.XWikiDocument.displayDocument(XWikiDocument.java:1488)
at com.xpn.xwiki.api.Document.displayDocument(Document.java:822)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.value(ASTReference.java:704)
at org.apache.velocity.runtime.parser.node.ASTExpression.value(ASTExpression.java:75)
at org.apache.velocity.runtime.parser.node.ASTSetDirective.render(ASTSetDirective.java:242)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:190)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.xwiki.velocity.internal.directive.TryCatchDirective.render(TryCatchDirective.java:86)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:856)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:811)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:803)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:79)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:73)
at org.xwiki.template.script.TemplateScriptService.render(TemplateScriptService.java:54)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.render(ASTReference.java:492)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.directive.VelocimacroProxy.render(VelocimacroProxy.java:217)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:331)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:261)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:856)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:811)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:803)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:79)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:73)
at org.xwiki.template.script.TemplateScriptService.render(TemplateScriptService.java:54)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.render(ASTReference.java:492)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.directive.VelocimacroProxy.render(VelocimacroProxy.java:217)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:331)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:261)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:171)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:190)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:849)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:835)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.render(DefaultTemplateManager.java:91)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.render(DefaultTemplateManager.java:85)
at com.xpn.xwiki.XWiki.evaluateTemplate(XWiki.java:2555)
at com.xpn.xwiki.web.Utils.parseTemplate(Utils.java:180)
at com.xpn.xwiki.web.XWikiAction.execute(XWikiAction.java:651)
at com.xpn.xwiki.web.XWikiAction.execute(XWikiAction.java:339)
at com.xpn.xwiki.web.LegacyActionServlet.service(LegacyActionServlet.java:111)
at jakarta.servlet.http.HttpServlet.service(HttpServlet.java:723)
at org.eclipse.jetty.ee11.servlet.ServletHolder$NotAsync.service(ServletHolder.java:1393)
at org.eclipse.jetty.ee11.servlet.ServletHolder.handle(ServletHolder.java:750)
at org.eclipse.jetty.ee11.servlet.ServletHandler$ChainEnd.doFilter(ServletHandler.java:1668)
at com.xpn.xwiki.web.ActionFilter.doFilter(ActionFilter.java:123)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.wysiwyg.filter.ConversionFilter.doFilter(ConversionFilter.java:71)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SetHTTPHeaderFilter.doFilter(SetHTTPHeaderFilter.java:66)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.resource.servlet.RoutingFilter.doFilter(RoutingFilter.java:135)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SavedRequestRestorerFilter.doFilter(SavedRequestRestorerFilter.java:212)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SafeRedirectFilter.doFilter(SafeRedirectFilter.java:106)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.ResolveRelativeRedirectFilter.doFilter(ResolveRelativeRedirectFilter.java:129)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SourceURLResolverFilter.doFilter(SourceURLResolverFilter.java:177)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SetCharacterEncodingFilter.doFilter(SetCharacterEncodingFilter.java:120)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:208)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.eclipse.jetty.ee11.websocket.servlet.WebSocketUpgradeFilter.doFilter(WebSocketUpgradeFilter.java:199)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.eclipse.jetty.ee11.servlet.ServletHandler$MappedServlet.handle(ServletHandler.java:1602)
at org.eclipse.jetty.ee11.servlet.ServletChannel.dispatch(ServletChannel.java:868)
at org.eclipse.jetty.ee11.servlet.ServletChannel.handle(ServletChannel.java:449)
at org.eclipse.jetty.ee11.servlet.ServletHandler.handle(ServletHandler.java:470)
at org.eclipse.jetty.security.SecurityHandler.handle(SecurityHandler.java:546)
at org.eclipse.jetty.ee11.servlet.SessionHandler.handle(SessionHandler.java:763)
at org.eclipse.jetty.server.handler.ContextHandler.handle(ContextHandler.java:1224)
at org.eclipse.jetty.server.handler.ContextHandlerCollection.handle(ContextHandlerCollection.java:178)
at org.eclipse.jetty.server.Server.handle(Server.java:197)
at org.eclipse.jetty.server.internal.HttpChannelState$HandlerInvoker.run(HttpChannelState.java:787)
at org.eclipse.jetty.server.internal.HttpConnection.onFillable(HttpConnection.java:410)
at org.eclipse.jetty.server.internal.HttpConnection$FillableCallback.succeeded(HttpConnection.java:1805)
at org.eclipse.jetty.io.FillInterest.fillable(FillInterest.java:105)
at org.eclipse.jetty.io.SelectableChannelEndPoint$1.run(SelectableChannelEndPoint.java:54)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.runTask(AdaptiveExecutionStrategy.java:492)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.epcRunTask(AdaptiveExecutionStrategy.java:428)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.consumeTask(AdaptiveExecutionStrategy.java:401)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.tryProduce(AdaptiveExecutionStrategy.java:255)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.run(AdaptiveExecutionStrategy.java:204)
at org.eclipse.jetty.util.thread.ReservedThreadExecutor$ReservedThread.run(ReservedThreadExecutor.java:317)
at org.eclipse.jetty.util.thread.QueuedThreadPool.runJob(QueuedThreadPool.java:1009)
at org.eclipse.jetty.util.thread.QueuedThreadPool$Runner.doRunJob(QueuedThreadPool.java:1239)
at org.eclipse.jetty.util.thread.QueuedThreadPool$Runner.run(QueuedThreadPool.java:1194)
at java.base/java.lang.Thread.run(Thread.java:1583)
BMX-Fahrräder sind speziell für das Gelände ausgelegte Sportgeräte. Für den profes-
sionellen Einsatz dieser Fahrräder wird auf horizontalem Untergrund eine 3 m breite
Sprungschanze installiert. Im Längsschnitt der Schanze kann deren Profillinie für
\(x ∈ \left[ −8;0 \right]\) modellhaft durch die in definierte Funktion f mit
beschrieben werden. Die Abbildung 1 zeigt den zugehörigen Teil des Graphen von f.
Der Startpunkt, von dem aus die Schanze durchfahren wird, wird durch den Punkt
\(S( −8 | f ( −8 ) )8,5 <= x <= 17,5\) dargestellt, der Absprungpunkt durch \(A(0 | f ( 0 ) )\).
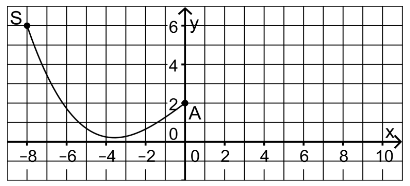
Abbildung 1
Veranschaulichen Sie in Abbildung 1 die mittlere Steigung der Schanze zwischen
Startpunkt und Absprungpunkt. Bestimmen Sie diese Steigung.
Unbekanntes Makro: tags. Klicke auf diese Nachricht, um Details zu erfahren.
Das Makro [tags] befindet sich nicht in der Liste der registrierten Makros. Überprüfen Sie die Schreibweise oder wenden Sie sich an Ihren Administrator.
Das Makro [aufgabe] konnte nicht ausgeführt werden. Grund: [Parameter [afb] is mandatory]. Klicke auf diese Nachricht, um Details zu erfahren.
org.xwiki.rendering.macro.parameter.MacroParameterException: Parameter [afb] is mandatory
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.validate(DefaultWikiMacro.java:222)
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.execute(DefaultWikiMacro.java:121)
at org.xwiki.rendering.wikimacro.internal.DefaultWikiMacro.execute(DefaultWikiMacro.java:61)
at org.xwiki.rendering.internal.transformation.macro.MacroTransformation.transform(MacroTransformation.java:441)
at org.xwiki.rendering.internal.transformation.DefaultRenderingContext.transformInContext(DefaultRenderingContext.java:183)
at org.xwiki.rendering.internal.transformation.DefaultTransformationManager.performTransformations(DefaultTransformationManager.java:88)
at org.xwiki.rendering.internal.transformation.XWikiTransformationManager.superPerformTransformations(XWikiTransformationManager.java:95)
at org.xwiki.rendering.internal.transformation.XWikiTransformationManager.performTransformations(XWikiTransformationManager.java:88)
at org.xwiki.display.internal.DocumentContentAsyncExecutor.executeInCurrentExecutionContext(DocumentContentAsyncExecutor.java:397)
at org.xwiki.display.internal.DocumentContentAsyncExecutor.execute(DocumentContentAsyncExecutor.java:269)
at org.xwiki.display.internal.DocumentContentAsyncRenderer.execute(DocumentContentAsyncRenderer.java:112)
at org.xwiki.rendering.async.internal.block.AbstractBlockAsyncRenderer.render(AbstractBlockAsyncRenderer.java:157)
at org.xwiki.rendering.async.internal.block.AbstractBlockAsyncRenderer.render(AbstractBlockAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:290)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.execute(DefaultBlockAsyncRendererExecutor.java:125)
at org.xwiki.display.internal.DocumentContentDisplayer.display(DocumentContentDisplayer.java:93)
at org.xwiki.display.internal.DocumentContentDisplayer.display(DocumentContentDisplayer.java:46)
at org.xwiki.display.internal.DefaultDocumentDisplayer.display(DefaultDocumentDisplayer.java:96)
at org.xwiki.display.internal.DefaultDocumentDisplayer.display(DefaultDocumentDisplayer.java:39)
at org.xwiki.sheet.internal.SheetDocumentDisplayer.display(SheetDocumentDisplayer.java:123)
at org.xwiki.sheet.internal.SheetDocumentDisplayer.display(SheetDocumentDisplayer.java:52)
at org.xwiki.display.internal.ConfiguredDocumentDisplayer.display(ConfiguredDocumentDisplayer.java:68)
at org.xwiki.display.internal.ConfiguredDocumentDisplayer.display(ConfiguredDocumentDisplayer.java:42)
at com.xpn.xwiki.doc.XWikiDocument.display(XWikiDocument.java:1433)
at com.xpn.xwiki.doc.XWikiDocument.getRenderedContent(XWikiDocument.java:1569)
at com.xpn.xwiki.doc.XWikiDocument.displayDocument(XWikiDocument.java:1519)
at com.xpn.xwiki.doc.XWikiDocument.displayDocument(XWikiDocument.java:1488)
at com.xpn.xwiki.api.Document.displayDocument(Document.java:822)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.value(ASTReference.java:704)
at org.apache.velocity.runtime.parser.node.ASTExpression.value(ASTExpression.java:75)
at org.apache.velocity.runtime.parser.node.ASTSetDirective.render(ASTSetDirective.java:242)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:190)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.xwiki.velocity.internal.directive.TryCatchDirective.render(TryCatchDirective.java:86)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:856)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:811)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:803)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:79)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:73)
at org.xwiki.template.script.TemplateScriptService.render(TemplateScriptService.java:54)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.render(ASTReference.java:492)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.directive.VelocimacroProxy.render(VelocimacroProxy.java:217)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:331)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:261)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:856)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:811)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderNoException(InternalTemplateManager.java:803)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:79)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.renderNoException(DefaultTemplateManager.java:73)
at org.xwiki.template.script.TemplateScriptService.render(TemplateScriptService.java:54)
at java.base/jdk.internal.reflect.DirectMethodHandleAccessor.invoke(DirectMethodHandleAccessor.java:103)
at java.base/java.lang.reflect.Method.invoke(Method.java:580)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.doInvoke(UberspectImpl.java:571)
at org.apache.velocity.util.introspection.UberspectImpl$VelMethodImpl.invoke(UberspectImpl.java:554)
at org.apache.velocity.runtime.parser.node.ASTMethod.execute(ASTMethod.java:221)
at org.apache.velocity.runtime.parser.node.ASTReference.execute(ASTReference.java:368)
at org.apache.velocity.runtime.parser.node.ASTReference.render(ASTReference.java:492)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.directive.VelocimacroProxy.render(VelocimacroProxy.java:217)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:331)
at org.apache.velocity.runtime.directive.RuntimeMacro.render(RuntimeMacro.java:261)
at org.apache.velocity.runtime.parser.node.ASTDirective.render(ASTDirective.java:304)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:171)
at org.apache.velocity.runtime.parser.node.ASTBlock.render(ASTBlock.java:147)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.runtime.parser.node.ASTIfStatement.render(ASTIfStatement.java:190)
at org.apache.velocity.runtime.parser.node.SimpleNode.render(SimpleNode.java:439)
at org.apache.velocity.Template.merge(Template.java:358)
at org.apache.velocity.Template.merge(Template.java:262)
at org.xwiki.velocity.internal.InternalVelocityEngine.evaluate(InternalVelocityEngine.java:233)
at com.xpn.xwiki.internal.template.VelocityTemplateEvaluator.evaluateContent(VelocityTemplateEvaluator.java:107)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.evaluateContent(TemplateAsyncRenderer.java:219)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.renderVelocity(TemplateAsyncRenderer.java:174)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:135)
at com.xpn.xwiki.internal.template.TemplateAsyncRenderer.render(TemplateAsyncRenderer.java:54)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.lambda$syncRender$0(DefaultAsyncRendererExecutor.java:284)
at com.xpn.xwiki.internal.security.authorization.DefaultAuthorExecutor.call(DefaultAuthorExecutor.java:98)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.syncRender(DefaultAsyncRendererExecutor.java:284)
at org.xwiki.rendering.async.internal.DefaultAsyncRendererExecutor.render(DefaultAsyncRendererExecutor.java:267)
at org.xwiki.rendering.async.internal.block.DefaultBlockAsyncRendererExecutor.render(DefaultBlockAsyncRendererExecutor.java:154)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:907)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:869)
at com.xpn.xwiki.internal.template.InternalTemplateManager.renderFromSkin(InternalTemplateManager.java:849)
at com.xpn.xwiki.internal.template.InternalTemplateManager.render(InternalTemplateManager.java:835)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.render(DefaultTemplateManager.java:91)
at com.xpn.xwiki.internal.template.DefaultTemplateManager.render(DefaultTemplateManager.java:85)
at com.xpn.xwiki.XWiki.evaluateTemplate(XWiki.java:2555)
at com.xpn.xwiki.web.Utils.parseTemplate(Utils.java:180)
at com.xpn.xwiki.web.XWikiAction.execute(XWikiAction.java:651)
at com.xpn.xwiki.web.XWikiAction.execute(XWikiAction.java:339)
at com.xpn.xwiki.web.LegacyActionServlet.service(LegacyActionServlet.java:111)
at jakarta.servlet.http.HttpServlet.service(HttpServlet.java:723)
at org.eclipse.jetty.ee11.servlet.ServletHolder$NotAsync.service(ServletHolder.java:1393)
at org.eclipse.jetty.ee11.servlet.ServletHolder.handle(ServletHolder.java:750)
at org.eclipse.jetty.ee11.servlet.ServletHandler$ChainEnd.doFilter(ServletHandler.java:1668)
at com.xpn.xwiki.web.ActionFilter.doFilter(ActionFilter.java:123)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.wysiwyg.filter.ConversionFilter.doFilter(ConversionFilter.java:71)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SetHTTPHeaderFilter.doFilter(SetHTTPHeaderFilter.java:66)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.resource.servlet.RoutingFilter.doFilter(RoutingFilter.java:135)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SavedRequestRestorerFilter.doFilter(SavedRequestRestorerFilter.java:212)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SafeRedirectFilter.doFilter(SafeRedirectFilter.java:106)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.ResolveRelativeRedirectFilter.doFilter(ResolveRelativeRedirectFilter.java:129)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SourceURLResolverFilter.doFilter(SourceURLResolverFilter.java:177)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.xwiki.container.servlet.filters.internal.SetCharacterEncodingFilter.doFilter(SetCharacterEncodingFilter.java:120)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:208)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.eclipse.jetty.ee11.websocket.servlet.WebSocketUpgradeFilter.doFilter(WebSocketUpgradeFilter.java:199)
at org.eclipse.jetty.ee11.servlet.FilterHolder.doFilter(FilterHolder.java:205)
at org.eclipse.jetty.ee11.servlet.ServletHandler$Chain.doFilter(ServletHandler.java:1640)
at org.eclipse.jetty.ee11.servlet.ServletHandler$MappedServlet.handle(ServletHandler.java:1602)
at org.eclipse.jetty.ee11.servlet.ServletChannel.dispatch(ServletChannel.java:868)
at org.eclipse.jetty.ee11.servlet.ServletChannel.handle(ServletChannel.java:449)
at org.eclipse.jetty.ee11.servlet.ServletHandler.handle(ServletHandler.java:470)
at org.eclipse.jetty.security.SecurityHandler.handle(SecurityHandler.java:546)
at org.eclipse.jetty.ee11.servlet.SessionHandler.handle(SessionHandler.java:763)
at org.eclipse.jetty.server.handler.ContextHandler.handle(ContextHandler.java:1224)
at org.eclipse.jetty.server.handler.ContextHandlerCollection.handle(ContextHandlerCollection.java:178)
at org.eclipse.jetty.server.Server.handle(Server.java:197)
at org.eclipse.jetty.server.internal.HttpChannelState$HandlerInvoker.run(HttpChannelState.java:787)
at org.eclipse.jetty.server.internal.HttpConnection.onFillable(HttpConnection.java:410)
at org.eclipse.jetty.server.internal.HttpConnection$FillableCallback.succeeded(HttpConnection.java:1805)
at org.eclipse.jetty.io.FillInterest.fillable(FillInterest.java:105)
at org.eclipse.jetty.io.SelectableChannelEndPoint$1.run(SelectableChannelEndPoint.java:54)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.runTask(AdaptiveExecutionStrategy.java:492)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.epcRunTask(AdaptiveExecutionStrategy.java:428)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.consumeTask(AdaptiveExecutionStrategy.java:401)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.tryProduce(AdaptiveExecutionStrategy.java:255)
at org.eclipse.jetty.util.thread.strategy.AdaptiveExecutionStrategy.run(AdaptiveExecutionStrategy.java:204)
at org.eclipse.jetty.util.thread.ReservedThreadExecutor$ReservedThread.run(ReservedThreadExecutor.java:317)
at org.eclipse.jetty.util.thread.QueuedThreadPool.runJob(QueuedThreadPool.java:1009)
at org.eclipse.jetty.util.thread.QueuedThreadPool$Runner.doRunJob(QueuedThreadPool.java:1239)
at org.eclipse.jetty.util.thread.QueuedThreadPool$Runner.run(QueuedThreadPool.java:1194)
at java.base/java.lang.Thread.run(Thread.java:1583)
Im Rahmen eines Tests läuft ein Sportler auf einem Laufband. Dabei wird bei ansteigender Geschwindigkeit jeweils die Konzentration sogenannter Laktate im Blut gemessen.
Die Abhängigkeit der Laktatkonzentration von der Geschwindigkeit kann für
\( 8,5 <= x <= 17,5\) modellhaft durch die Funktion k mit
\(k( x )= {1} over {40}(x^{3} -30x^{2}+288x -815)\)beschrieben werden.
Dabei ist x die Geschwindigkeit des Sportlers in Kilometer pro Stunde und k die Laktatkonzentration in Millimol pro Liter
\({mmol} over {l} \).
Berechnen Sie im Modell für den Geschwindigkeitsbereich von 12 bis 17,5
\({km} over {h}\) die mittlere Änderungsrate der Laktatkonzentration.
