BPE 6.2 Änderungsraten bestimmen
K1 K4 Ich kann die durchschnittliche Änderungsrate als Steigung der Sekante deuten
K4 K5 Ich kann die durchschnittliche Änderungsrate grafisch aus einem Funktionsgraphen bestimmen
K5 Ich kann die durchschnittliche Änderungsrate algebraisch aus einem Funktionsterm bestimmen
K4 K5 Ich kann die durchschnittliche Änderungsrate aus einer Wertetabelle bestimmen
K4 K5 Ich kann die momentane Änderungsrate als Steigung der Tangente grafisch bestimmen
1 Änderungsrate Intervall (4 min) 𝕋 𝕃
Berechne die durchschnittliche Änderungsrate der Funktion f im Intervall \(\left[-3;2\right]\).
- \(f(x)=5x^2-3\)
- \(f(x)=2^x\)
| AFB I - K5 | Quelle Martina Wagner |
2 Rechnerisch und graphisch (20 min) 𝕋 𝕃
Gegeben ist die Funktion f mit \(f(x)=-0,5x^2\cdot (x-4)\) für \(x\in \mathbb{R}\). Ihr Schaubild ist \(K_f\).
Bestimme die mittlere Änderungsrate für das Intervall [1; 4] rechnerisch und graphisch.
| AFB I - K5 | Quelle Martin Stern, Dirk Tebbe |
3 Aus Wertetabelle (5 min) 𝕃
Berechne jeweils die durchschnittliche Änderungsrate für die Intervalle \(\left[0;2\right]\) und \(\left[1;3\right]\).
| x | 0 | 1 | 2 | 3 |
| y | 1 | 2 | 4 | 8 |
| AFB I - K5 | Quelle Martin Stern, Dirk Tebbe |
4 Funktionsterms aus Differenzenquotient (15 min) 𝕃
Bestimme jeweils den Funktionsterm für die Funktion g, so dass gilt: \(\overline{m}=\frac{g(4)-g(2)}{4-2}=2\)
- für \(g(x)=mx\)
- für \(g(x)=ax^2\)
| AFB I - K5 | Quelle Martin Stern, Dirk Tebbe |
5 Änderungsrate offenes Intervall (10 min) 𝕃
Gegeben ist die Funktion f mit \(f(x)=x^2\) im Intervall \(\left[-1;b\right]\). Ermittle einen Punkt P(b|\(f(b)\)), der folgende Bedingung erfüllt:
\(m_s=\frac{f(b)-1}{b+1}=1,5\)
| AFB II - K5 | Quelle Martin Stern, Dirk Tebbe |
6 Tidenhub (7 min) 𝕃
Das Schaubild zeigt den Pegelstand f(t) in dm an der Hafeneinfahrt einer Küstenstadt in Abhängigkeit von der Zeit t in h. Dabei ist t=0 der Beobachtungsbeginn.
| t | 0 | 0,5 | 1 | 1,5 | 2 | 3 | 4 | 4,5 | 5 | 5,5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| f(t) | 40 | 45,2 | 50 | 54,1 | 57,3 | 60 | 57,3 | 54,1 | 50 | 45,2 | 40 |
- Bestimme die mittlere Änderungsrate des Pegelstands in Zeitintervallen [0,5; 1,5] und [4,5; 5,5].
- Gib die mittlere Änderungsrate des Pegelstands im Intervall [1; 5] an.
- Erläutere die Bedeutung der Steigung der Tangenten in P.
| AFB I - K4 K5 K6 | Quelle Holger Engels, Martina Wagner |
7 Bewegung (11 min) 𝕃
Die Bewegung eines Körpers wird für die ersten 9 Sekunden ab Beobachtungsbeginn näherungsweise durch eine Potenzfunktion beschrieben.
Begründe, ob die folgenden Aussagen wahr oder falsch sind.
- Es gibt kein Intervall, in dem die mittlere Geschwindigkeit null ist.
- Die mittlere Geschwindigkeit im Intervall [4; 8] beträgt 0,5 m/s.
- Die momentane Geschwindigkeit zum Zeitpunkt t=8 beträgt 4 m/s.
- Die momentane Geschwindigkeit ist zu keinem Zeitpunkt größer als 1 m/s.
- Die momentane Geschwindigkeit zum Zeitpunkt t=0 ist 0 m/s.
| AFB II - K1 K4 K5 K6 | Quelle Holger Engels, Martina Wagner |
8 Aktienkurs (10 min) 𝕃
Die Abbildung zeigt den Tagesverlauf des Wirecardaktienkurs am 19.06.2020 von 8:00 Uhr bis 10:00 Uhr. Der Aktienkurs ist an diesem Tag aufgrund des in einen Bilanzskandal verwickelten Dax-Konzerns um 45% gesunken.
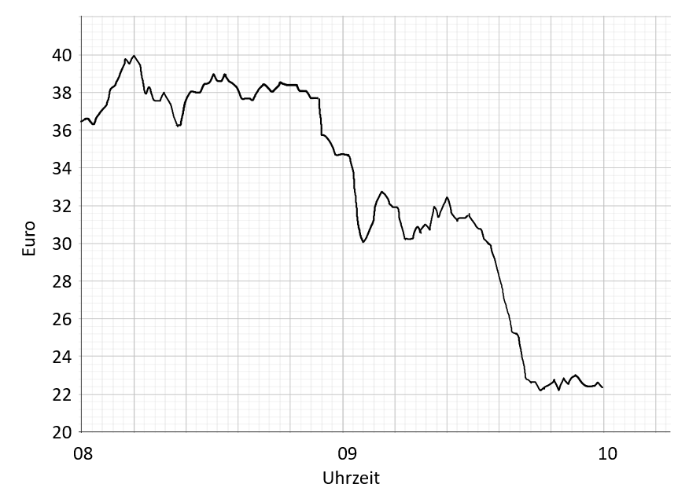
- Beschreibe grob den Kursverlauf in den zwei Stunden.
- Berechne näherungsweise die durchschnittliche Änderungsrate zwischen 9:30 uhr und 9:45 Uhr und vergleiche diese mit der momentanen Änderungsrate um 9:45 Uhr.
- Welchen Wertverlust erlitt die Aktie innerhalb der zwei Stunden? Überprüfe den oben genannten prozentualen Wertverlust
- Zu welchem Zeitpunkt ist der Wertverlust am größten?
| AFB II - K1 K2 K2 K6 | Quelle Simone Kanzler, Stephanie Wietzorek |
9 BMX (10 min) 𝕃
BMX-Fahrräder sind speziell für das Gelände ausgelegte Sportgeräte. Für den professionellen Einsatz dieser Fahrräder wird auf horizontalem Untergrund eine 3 m breite Sprungschanze installiert. Im Längsschnitt der Schanze kann deren Profillinie für \(x \in\left[ -8;0 \right]\) modellhaft durch die in \(\mathbb{R}\) definierte Funktion f mit
beschrieben werden. Die Abbildung 1 zeigt den zugehörigen Teil des Graphen von f.
Der Startpunkt, von dem aus die Schanze durchfahren wird, wird durch den Punkt \(S( -8 | f ( -8 ) )\) dargestellt, der Absprungpunkt durch \(A(0 | f ( 0 ) )\).
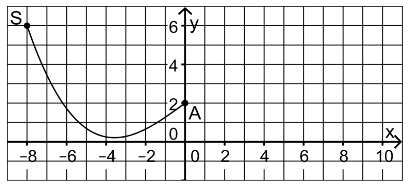
Abbildung 1
Veranschauliche in Abbildung 1 die mittlere Steigung der Schanze zwischen Startpunkt und Absprungpunkt. Bestimme diese Steigung.
| AFB I - K2 K5 | Quelle IQB e.V. 2019 Analysis gAN Teil 2 CAS | |
| Links Interaktiv erkunden | ||
10 Laufband (8 min) 𝕃
Im Rahmen eines Tests läuft ein Sportler auf einem Laufband. Dabei wird bei ansteigender Geschwindigkeit jeweils die Konzentration sogenannter Laktate im Blut gemessen.
Die Abhängigkeit der Laktatkonzentration von der Geschwindigkeit kann für \(8,5\leq x \leq 17,5\) modellhaft durch die Funktion k beschrieben werden mit:
Dabei ist \(x\) die Geschwindigkeit des Sportlers in Kilometer pro Stunde und k die Laktatkonzentration in Millimol pro Liter \(\frac{mmol}{l}\). Berechne im Modell für den Geschwindigkeitsbereich von 12 bis 17,5 \(\frac{km}{h}\) die mittlere Änderungsrate der Laktatkonzentration.
| AFB II - K3 K5 | Quelle IQB e.V. 2019 Analysis gAN Teil 2 WTR |
11 Kondensator (8 min) 𝕃
Ein Kondensator ist ein Bauteil, das elektrische Ladung speichert. Der Ladevorgang eines Kondensators wird im Labor untersucht. Zum Zeitpunkt t = 0 beginnt der Aufladevorgang. Die Stärke des elektrischen Stroms, der beim Aufladen fließt, wird gemessen. Die Messwerte sind in folgender Tabelle zusammengefasst:
| Zeit [s] | 1,0 | 2,4 | 4,8 | 7,2 | 9,6 |
|---|---|---|---|---|---|
| Stromstärke [mA] | 9,0 | 6,0 | 3,0 | 1,5 | 0,75 |
Ermittle einen Zeitraum beim Ladevorgang, in der die durchschnittliche Änderungsrate der Stromstärke halb so groß ist wie im Zeitraum von 2,4 s bis 4,8 s!
| AFB II - K2 K4 K5 | Quelle Abi 2012 Anwendung, modifiziert |
12 Von der Sekante zur Tangente (15 min) 𝕀 𝕃
Gegeben ist eine Normalparabel mit einem festen Punkt A(1|f(1)) und einem auf der Normalparabel beliebigem Punkt B(1+h|f(1+h)).
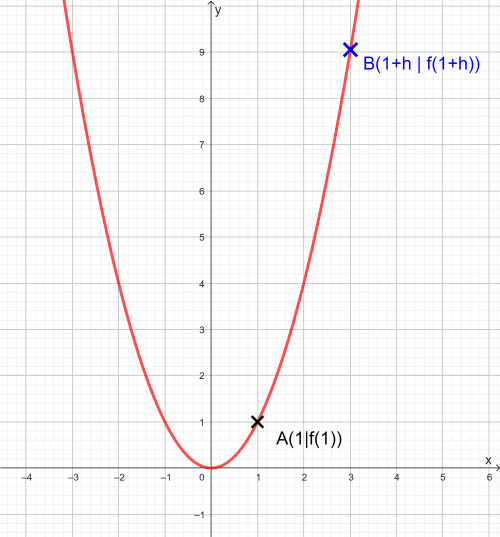
- Bestimme die Koordinaten des Punktes B für h = 2 und berechne die Steigung der Sekanten zwischen A und B.
- Gib eine allgemeine Formel für die Steigung der Sekanten zwischen A und dem beliebigem Punkt B an.
- Beschreibe, wie sich die Lage von B verändert, wenn h immer kleiner wird (h geht gegen 0)
- Berechne die Sekantensteigung für h = 0,1.
- Die Tangente im Punkt A besitzt die Gleichung \(y = 2x - 1\). Stelle einen Zusammenhang zwischen der Steigung der Sekanten und der Tangentensteigung in Abhängigkeit von h auf.
| AFB III - K1 K2 K5 K6 | Quelle Simone Kanzler, Stephanie Wietzorek |
Inhalt für Lehrende (Anmeldung erforderlich)
