BPE 7 Einheitsübergreifend
1 Grundriss (5 min) 𝕃
Gegeben sind die Eckpunkte \(A(2,5|0|0), B(2,5|3|0), C(3,5|3|0),D(3,5|4|0), E(0|4|0), F(0|-3|0),G(5|-3|0), H(5|0|0)\) des Grundriss einer Wohnung.
- Zeichne den Grundriss der Wohnung mit Hilfe der Punkte in ein dreidimensionales Koordinatensystem ein.
- Berechne die Größe dieser Wohnung, wenn eine Längeneinheit einem Meter entspricht.
| AFB I - K3 K5 | Quelle Martina Wagner, Caroline Leplat, Dirk Tebbe | #Martina Wagner# Caroline Leplat# Dirk Tebbe |
2 Pyramide (15 min) 𝕃
Gegeben ist eine Pyramide mit quadratischer Grundfläche. Die Punkte \(A(12|0|2), B(12|8|2),C(4|8|2)\) sind Eckpunkte der Grundfläche. \( S(8|4|7,5)\) ist die Spitze der Pyramide.
- Zeichne die Pyramide in ein dreidimensionales Koordinatensystem und gib die Koordinaten von Punkt D an.
- Bestimme den Mittelpunkt M der Grundfläche der Pyramide.
- Zeige, dass es sich um eine quadratische Grundfläche handelt.
- Erläutere die geometrische Bedeutung von \(\vec{MA}\cdot\vec{MS}=0\).
- Untersuche, welche besondere Lage die Grundfläche der Pyramide im Koordinatensystem hat.
| AFB II - K1 K4 K5 | Quelle Martina Wagner, Caroline Leplat, Dirk Tebbe | #Martina Wagner# Caroline Leplat# Dirk Tebbe |
3 Würfel (15 min) 𝕃
Die Punkte \(A(0|0|0), B(5|0|0), C(5|5|0)\) und \(H(0|0|5)\) bilden die Eckpunkte eines Würfels.
- Bestimme, die fehlenden Koordinaten der Punkte D, E und G des Würfels und skizziere diesen in ein dreidimensionales Koordinatensystem.
- Zeige, dass das Volumen des Würfels 125 Volumeneinheiten beträgt.
- Das Volumen einer Pyramide berechnet sich durch die Formel \(V=\frac{1}{3} \cdot G\cdot h\)
Skizziere in ein dreidimensionales Koordinatensystem eine Pyramide mit dreieckiger Grundfläche, die das gleiche Volumen wie der Würfel besitzt. Gib die Eckpunkte deiner Pyramide an.
| AFB II - K1 K2 K4 K5 | Quelle Martina Wagner, Caroline Leplat, Dirk Tebbe | #Martina Wagner# Caroline Leplat# Dirk Tebbe |
4 Winkel (5 min) 𝕃
Der Vektor \(\vec{a}\) mit der Länge 2 cm und der Vektor \(\vec{b}\) mit der Länge 3 cm schließen einen Winkel \(\alpha\) ein. Begründe, dass die Gegenvektoren von \(\vec{a}\) und \(\vec{b}\) den gleichen Winkel einschließen.
| AFB II - K1 K5 | Quelle Martina Wagner, Caroline Leplat, Dirk Tebbe | #Martina Wagner# Caroline Leplat# Dirk Tebbe |
5 Richtungsvektor (5 min) 𝕃
- Benenne die in der Figur erkennbaren Vektoren.
- Zeige, dass die beiden Gleichungen
\(\vec{AB}=-(\vec{a}-\vec{b})\) und
\(\vec{AB}=\vec{OB}-\vec{OA}\) den gleichen Richtungsvektor beschreiben.
| AFB II - K1 K5 | Quelle Martina Wagner, Caroline Leplat, Dirk Tebbe | #Martina Wagner# Caroline Leplat# Dirk Tebbe |
6 Nachweis Quader (10 min) 𝕃
Die Vektoren \(\vec{a}= \left(\begin{array}{c} 2 \\ 1 \\ 2 \end{array}\right)\),\(\vec{b}= \left(\begin{array}{c} -1 \\ 2 \\ 0 \end{array}\right)\) und \(\vec{c_t}= \left(\begin{array}{c} 4t \\ 2t \\ -5t \end{array}\right)\) spannen für jeden Wert von \( t \in \mathbb{R}\setminus\{0\}\) einen Körper auf. Die Abbildung zeigt den Sachverhalt beispielhaft für einen Wert von \(t\).
- Zeige, dass die aufgespannten Körper Quader sind.
- Bestimme diejenigen Werte von \(t\), für die der zugehörige Quader das Volumen 15 besitzt.
| AFB II - K1 K2 K5 | Quelle IQB | #iqb |
7 Berechnungen am Quader (10 min) 𝕃
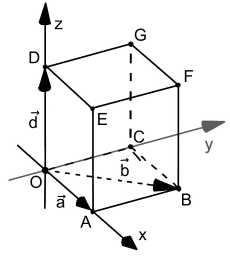 Die Abbildung zeigt einen Quader sowie die Ortsvektoren der Eckpunkte \(A, B\) und \(D\). Die Grundfläche \(OABC\) des Quaders ist quadratisch.
Die Abbildung zeigt einen Quader sowie die Ortsvektoren der Eckpunkte \(A, B\) und \(D\). Die Grundfläche \(OABC\) des Quaders ist quadratisch.
- Beschreibe die Lage des Punkts, zu dem der Ortsvektor \(\frac{1}{2}\cdot (\vec{b}-\vec{a})\) gehört.
Der Punkt \(P\) hat den Ortsvektor \(\frac{1}{2}\vec{b}+ \vec{d}\).
- Zeichne \(P\) in die Abbildung ein.
- Begründe, dass der Wert des Terms \(\vec{b} \circ \overline{OP}\) nur von der Seitenlänge der Grundfläche abhängt.
| AFB III - K1 K2 K4 K5 K6 | Quelle IQB | #iqb |
8 Rasenfläche (40 min) 𝕃
Die Punkte \(A(0|0|0), B(18|0|1,5), C(12|10|1), D(12|15|1)\) und \(E(0|15|0)\) stellen modellhaft die Eckpunkte einer ebenen Rasenfläche dar (vgl. Abbildung). Die Strecken \(\overline{AB}\) und \(\overline{DE}\) sind parallel.
Im verwendeten Koordinatensystem entspricht eine Längeneinheit einem Meter in der Wirklichkeit.
- Zeige, dass auch \(\overline{AE}\) und \(\overline{CD}\) parallel sind und dass \(\overline{CD}\) und \(\overline{DE}\) einen rechten Winkel einschließen.
- Ausgehend vom Ansatz \(|\overline{AE}| \cdot |\overline{DE}| + \frac{1}{2}\cdot (|\overline{AB}|- |\overline{DE}|)\cdot\bigl(|\overline{AE}|-|\overline{CD}|\bigl) \) kann eine Größe berechnet werden, die im betrachteten Sachzusammenhang eine Rolle spielt. Nenne diese Größe und erläutere den gegebenen Ansatz.
Die Rasenfläche wird von einem Roboter gemäht, der die Form eines flachen Zylinders hat. Zur Beschreibung der Bewegung des Roboters wird der Mittelpunkt seiner kreisförmigen Unterseite betrachtet, die einen Radius von 20 cm hat. Es soll vereinfachend davon ausgegangen werden, dass dieser Mittelpunkt die Rasenfläche berührt. Die Position des Mittelpunkts wird zunächst durch \(P(3,6|8|0,3)\) dargestellt (vgl. Abbildung). Die anschließende Bewegung des Mittelpunkts verläuft im Modell entlang der Gerade \(g\), die durch \(P\) verläuft und den Richtungsvektor \(\vec{a}= \left(\begin{array}{c} 12 \\ -4 \\ 1 \end{array}\right)\) hat. Dabei bewegt sich der Roboter auf den durch \(\overline{BC}\) dargestellten Rand der Rasenfläche zu.
- Berechne die Koordinaten des Punkts \(Q\), in dem \(g\) die Strecke \(\overline{BC}\) schneidet. (zur Kontrolle: \(Q(15,6|4|1,3)\) )
- Weise nach, dass der Winkel, unter dem sich der Roboter dem Rand der Rasenfläche nähert, etwa 41° groß ist.
- Der Roboter ändert seine Richtung, sobald der Rand seiner Unterseite den Rand der Rasenfläche erreicht. Der Punkt, der die Position des Mittelpunkts im Moment der Richtungsänderung darstellt, wird mit \( S \) bezeichnet. Berechne mithilfe einer geeigneten Skizze die Koordinaten von \(S\).
| AFB III - K1 K2 K3 K4 K5 K6 | Quelle IQB | #iqb |
9 Ähnlichkeit und Strahlensätze (7 min) 𝕃
Die nicht maßstabsgetreue Abbildung zeigt das Quadrat \(ABCD\). Die Gerade \(g\), die durch \(B\) und den Mittelpunkt \(M\) der Seite \(\overline{AD}\) verläuft, hat den Richtungsvektor \(\vec{v}\). Der Punkt \(F\) ist der Fußpunkt des Lots von \(A\) auf \(g\).
- Begründe, dass \(|\overline{BF}|=2\cdot |\overline{AF}|\) gilt.
- Gib einen Term an, mit dem man die Koordinaten von \(B\) bestimmen könnte, wenn die Koordinaten von \(A\) und \(F\) sowie die Komponenten von \( \vec{v}\) bekannt wären.
| AFB III - K1 K2 K4 | Quelle IQB | #iqb |
10 Dreieck Koordinaten (6 min) 𝕃
Gegeben sind die Punkte \( A(5|0|a)\) und \(B(2|4|5)\). Der Koordinatenursprung wird mit \(O\) bezeichnet.
- Bestimme denjenigen Wert von \( a\), für den \(A\) und \(B\) den Abstand 5 haben.
- Ermittle denjenigen Wert von \( a\), für den das Dreieck \(OAB\) im Punkt \(B\) rechtwinklig ist.
| AFB II - K2 K5 | Quelle IQB | #iqb |
Inhalt für Lehrende (Anmeldung erforderlich)
