Zum Inhalt springen

Lösung Schwerpunkt im Dreieck

Version 4.1 von akukin am 2024/05/19 19:41

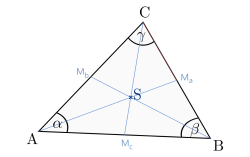
Schwerpunktlsg.png
Sei M_a der Mittelpunkt der Strecke \overline{BC}, M_b der Mittelpunkt der Strecke \overline{AC} und M_c der Mittelpunkt der Strecke \overline{AB}.

Es gilt:

\begin{align*} \overrightarrow{AS}&=k\cdot \overrightarrow{AM_a} \\ &= k\cdot \left(\overrightarrow{AB}+\frac{1}{2} \overrightarrow{BC}\right) \quad \text{(I)} \end{align*}

und

\begin{align*} \overrightarrow{CS}&=t\cdot \overrightarrow{CM_c} \\ &= t\cdot \left(\overrightarrow{CB}+\frac{1}{2} \overrightarrow{BA}\right) \quad \text{(II)} \end{align*}

Die Strecke \overrightarrow{AS} lässt sich als geschlossener Vektorzug wie folgt aufschreiben:
\begin{align*} \overrightarrow{AS}&=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CS} \\ \Leftrightarrow \overrightarrow{CS} &= \overrightarrow{AS}-\overrightarrow{AB}-\overrightarrow{BC} \quad \text{(III)} \end{align*}