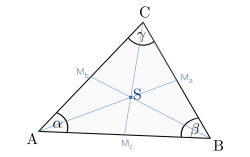
Sei \(M_a\) der Mittelpunkt der Strecke \( \overline{BC}\), \(M_b\) der Mittelpunkt der Strecke \( \overline{AC}\) und \(M_c\) der Mittelpunkt der Strecke \( \overline{AB}\).
Es gilt:
\[\begin{align*}
\overrightarrow{AS}&=k\cdot \overrightarrow{AM_a} \\
&= k\cdot \left(\overrightarrow{AB}+\frac{1}{2} \overrightarrow{BC}\right) \quad \text{(I)}
\end{align*}\]
und
\[\begin{align*}
\overrightarrow{CS}&=t\cdot \overrightarrow{CM_c} \\
&= t\cdot \left(\overrightarrow{CB}+\frac{1}{2} \overrightarrow{BA}\right) \quad \text{(II)}
\end{align*}\]
mit \(k,t \in \mathbb{R^+}\)
Die Strecke \(\overrightarrow{AS}\) lässt sich als geschlossener Vektorzug wie folgt aufschreiben:
\[\begin{align*}
\overrightarrow{AS}&=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CS} \\
\Leftrightarrow \overrightarrow{CS} &= \overrightarrow{AS}-\overrightarrow{AB}-\overrightarrow{BC} \quad \text{(III)}
\end{align*}\]
Einsetzen von \(\text{(I)}\) und \(\text{(II)}\) in \(\text{(III)}\):
\[\begin{align*}
&t\cdot \left(\overrightarrow{CB}+\frac{1}{2} \overrightarrow{BA}\right) = k\cdot \left(\overrightarrow{AB}+\frac{1}{2} \overrightarrow{BC}\right)-\overrightarrow{AB}-\overrightarrow{BC}\\
\Leftrightarrow &\overrightarrow{AB}\cdot \left(-\frac{1}{2}t-k+1\right)+\overrightarrow{BC}\cdot \left(-t-\frac{1}{2}k+1 \right)=0
\end{align*}\]
Da \(\overrightarrow{AB}\) und \(\overrightarrow{BC}\) linear unabhängig sind, ist die linke Seite genau dann 0, wenn die Terme innerhalb der Klammern beide 0 sind. Das heißt, man erhält folgendes Gleichungssystem:
\[\begin{align*}
\left(-\frac{1}{2}t-k+1\right)&=0 \quad (I) \\
\left(-t-\frac{1}{2}k+1 \right)&=0 \quad (II)
\end{align*}\]
\(2\cdot \text{(I)}\)-\(\text{(II)}\): \(-\frac{3}{2}k+1=0 \Leftrightarrow k=\frac{2}{3} \)
Einsetzen von \(k=\frac{2}{3}\) in \(\text{(I)}\) (oder \(\text{(II)}\)) liefert \(t=\frac{2}{3}\)

