Zum Inhalt springen

Lösung Schwerpunkt im Dreieck

Version 6.2 von akukin am 2024/05/19 18:23
  1. Für die Koordinaten des Schwerpunktes gilt:
    \(x_S=\frac{x_A+x_B+x_C}{3}=\frac{0+2+(-1)}{3}=\frac{1}{3}; \)
    \(y_S=\frac{y_A+y_B+y_C}{3}=\frac{0+3+5}{3}=\frac{8}{3};\)
    \(z_S=\frac{z_A+z_B+z_C}{3}=\frac{0+4+(-2)}{3}=\frac{2}{3}\)
    Somit: \(S\left(\frac{1}{3}|\frac{8}{3}|\frac{2}{3}\right)\)

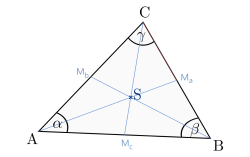
2. Schwerpunktlsg.png
Sei \(M_a\) der Mittelpunkt der Strecke \( \overline{BC}\), \(M_b\) der Mittelpunkt der Strecke \( \overline{AC}\) und \(M_c\) der Mittelpunkt der Strecke \( \overline{AB}\).

Es gilt:

\[\begin{align*} \overrightarrow{AS}&=k\cdot \overrightarrow{AM_a} \\ &= k\cdot \left(\overrightarrow{AB}+\frac{1}{2} \overrightarrow{BC}\right) \quad \text{(I)} \end{align*}\]

und

\[\begin{align*} \overrightarrow{CS}&=t\cdot \overrightarrow{CM_c} \\ &= t\cdot \left(\overrightarrow{CB}+\frac{1}{2} \overrightarrow{BA}\right) \quad \text{(II)} \end{align*}\]

mit \(k,t \in \mathbb{R^+}\)

Die Strecke \(\overrightarrow{AS}\) lässt sich als geschlossener Vektorzug wie folgt aufschreiben:

\[\begin{align*} \overrightarrow{AS}&=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CS} \\ \Leftrightarrow \overrightarrow{CS} &= \overrightarrow{AS}-\overrightarrow{AB}-\overrightarrow{BC} \quad \text{(III)} \end{align*}\]

Einsetzen von \(\text{(I)}\) und \(\text{(II)}\) in \(\text{(III)}\):

\[\begin{align*} &t\cdot \left(\overrightarrow{CB}+\frac{1}{2} \overrightarrow{BA}\right) = k\cdot \left(\overrightarrow{AB}+\frac{1}{2} \overrightarrow{BC}\right)-\overrightarrow{AB}-\overrightarrow{BC}\\ \Leftrightarrow &\overrightarrow{AB}\cdot \left(-\frac{1}{2}t-k+1\right)+\overrightarrow{BC}\cdot \left(-t-\frac{1}{2}k+1 \right)=0 \end{align*}\]

Da \(\overrightarrow{AB}\) und \(\overrightarrow{BC}\) linear unabhängig sind, ist die linke Seite genau dann 0, wenn die Terme innerhalb der Klammern beide 0 sind. Das heißt, man erhält folgendes Gleichungssystem:

\[\begin{align*} \left(-\frac{1}{2}t-k+1\right)&=0 \quad (i) \\ \left(-t-\frac{1}{2}k+1 \right)&=0 \quad (ii) \end{align*}\]

\(2\cdot \text{(i)}\)-\(\text{(ii)}\): \(-\frac{3}{2}k+1=0 \Leftrightarrow k=\frac{2}{3} \)

Einsetzen von \(k=\frac{2}{3}\) in \(\text{(i)}\) (oder \(\text{(ii)}\)) liefert \(t=\frac{2}{3}\).

Somit ist gezeigt, dass der Schwerpunkt \(S\) die Seitenhalbierenden im Verhältnis 2:1 teilt.

Die Koordinaten des Schwerpunktes erhält man, indem man \(k=\frac{2}{3}\) in Gleichung \(\text{(I)}}\) einsetzt.