BPE 10.4 Aufstellen von Funktionstermen
K4 K5 Ich kann aus grafisch gegebenen Funktionseigenschaften den Funktionsterm einer allgemeinen Sinus- bzw. Kosinusfunktion bestimmen
K4 K5 Ich kann aus tabellarisch gegebenen Funktionseigenschaften den Funktionsterm einer allgemeinen Sinus- bzw. Kosinusfunktion bestimmen
K4 K5 Ich kann aus verbal gegebenen Funktionseigenschaften den Funktionsterm einer allgemeinen Sinus- bzw. Kosinusfunktion bestimmen
Aufgabe 1 Funktionsterm aus Schaubild 𝕃
Das Schaubild zeigt die Graphen von einer Sinus- und einer Kosinusfunkion.
Bestimme jeweils einen passenden Funktionsterm bzw.
.
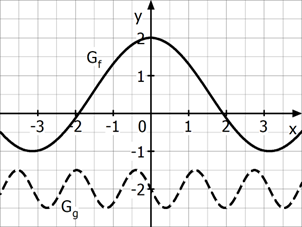
Schaubild 1
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 10 min |
| Quelle Dennis Löblich | Lizenz CC BY-SA | |
Aufgabe 2 Funktionsterme aus Eigenschaften 𝕃
Eine trigonometrische Funktion hat die Amplitude 5 und die Periode 4. Das Schaubild der Funktion hat einen Hochpunkt bei H(0|4).
Bestimme zwei passende Funktionsterme bzw.
.
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 10 min |
| Quelle Dennis Löblich | Lizenz CC BY-SA | |
Aufgabe 3 Gleicher Funktionswert 𝕃
Von einer allgemeinen cos-Funktion ist bekannt, dass sie im Intervall [0;10] nur an den Stellen x ∈ {1, 3, 7, 9} den Funktionswert 1 hat. Bestimme einen möglichen Funktionsterm.
| AFB III | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Holger Engels | Lizenz CC BY-SA | |
Aufgabe 4 Sinus als Kosinus
Gib an, wie die Funkion mit cos ausgedrückt werden kann.
| AFB I | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Holger Engels | Lizenz CC BY-SA | |
Aufgabe 5 Sinusparameter bestimmen (eAN) 𝕃
Betrachtet wird die in definierte Funktion
mit
. Die Punkte
und
sind direkt aufeinanderfolgende Extrempunkte des Graphen von
.
Bestimme die Werte von und
.
| AFB II | Kompetenzen K1 K2 K5 | Bearbeitungszeit k.A. |
| Quelle IQB e.V. | Lizenz CC BY | |
Aufgabe 6 Kosinusfunktion aufstellen (eAN) 𝕃
Eine in definierte Kosinusfunktion
hat die Periode
. Der Punkt
ist ein Hochpunkt des Graphen von
, der Punkt
ein Wendepunkt.
Bestimme eine Funktionsgleichung der Kosinusfunktion in Abhängigkeit von .
| AFB k.A. | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle IQB e.V. | Lizenz CC BY | |
Kompetenzmatrix und Seitenreflexion
| K1 | K2 | K3 | K4 | K5 | K6 | |
|---|---|---|---|---|---|---|
| I | 0 | 0 | 0 | 0 | 0 | 0 |
| II | 1 | 1 | 0 | 2 | 3 | 0 |
| III | 0 | 0 | 0 | 0 | 0 | 0 |
| Abdeckung Bildungsplan | ||
|---|---|---|
| Abdeckung Kompetenzen | ||
| Abdeckung Anforderungsbereiche | ||
| Eignung gemäß Kriterien | ||
| Umfang gemäß Mengengerüst |
