BPE 12.5 Tangente in Kurvenpunkt

Aufgabe 1  Tangente Funktionsschar (eAN) 𝕋  𝕃

Gegeben ist für jede positive reelle Zahl \(a\) die in \(\mathbb{R}\) definierte Funktion \(f_a\) mit \(f_a\left(x\right)=a\cdot x^2\). Die Abbildung zeigt den Graphen von \(f_\frac{1}{2}\) sowie die Tangente \(t\) an den Graphen von \(f_\frac{1}{2}\) im Punkt \(\left(4\middle| f_\frac{1}{2}\left(4\right)\right)\).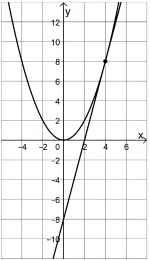

1. Gib anhand der Abbildung eine Gleichung der Tangente \(t\) an.
2. Weise nach, dass für jeden Wert \(u\in\mathbb{R}\) die Tangente an den Graphen von \(f_a\) im Punkt \(\left(u\middle| f_a\left(u\right)\right)\) die y-Achse im Punkt \(\left(0\middle|-f_a\left(u\right)\right)\) schneidet.
     

  

 
 
 
 
Hinweis:
Der Begriff „Schar“ beziehungsweise „Funktionsschar“ ist nicht konform zum Bildungsplan für berufliche Gymnasien in Baden-Württemberg. Deswegen wäre eine derartige Aufgabe für die Abiturprüfung an beruflichen Gymnasien nicht zulässig.

Eine bildungsplankonforme Variante wäre zum Beispiel:
Gegeben ist die in \(\mathbb{R}\) definierte Funktion \(f\) mit \(f\left(x\right)=\frac{1}{2}\cdot x^2\).
Die Abbildung zeigt den Graphen von \(f\) sowie die Tangente \(t\) an den Graphen von \(f\) im Punkt \(\left(4\middle| f\left(4\right)\right)\).

1. Gib anhand der Abbildung eine Gleichung der Tangente \(t\) an.
2. Der Graph von \(f\) wird in y-Richtung gestreckt; dabei entsteht der Graph der transformierten Funktion \(g\).
   Weise nach, dass unabhängig vom Streckungsfaktor für jeden Wert \(u\in\mathbb{R}\) die an den gestreckten Graphen im Punkt \(\left(u\middle| g\left(u\right)\right)\) angelegte Tangente die y-Achse im Punkt \(\left(0\middle|-g\left(u\right)\right)\) schneidet.

#iqb