BPE 12.5 Tangente in Kurvenpunkt
K5 Ich kann eine Gleichung der Tangente in einem gegebenen Punkt eines Funktionsgraphen bestimmen
K5 Ich kann prüfen, ob eine gegebene Gerade Tangente an einem Funktionsgraphen ist
1 Tangente in einem Kurvenpunkt (10 min) 𝕃
Gegeben ist die in \(\mathbb{R}\) definierte Funktion \(f\) mit \(f\left(x\right)=\frac{1}{5} x^3-\frac{16}{5}x\).
- Berechne die Gleichung der Tangente \(t\) an die Kurve \(K_f\) an der Stelle \(x=3\).
- Begründe, dass die Gerade \(g\) mit \(g(x)=\frac{11}{5}x+\frac{54}{5}\) auch Tangente an die Kurve \(K_f\) ist.
| AFB II - K1 K5 | Quelle Dirk Tebbe, Martin Stern |
2 Tangente in einem Kurvenpunkt II (k.A.) 𝕃
Gegeben ist die in \(\mathbb{R}\) definierte Funktion \(f\) mit \(f\left(x\right)=4-\frac{1}{2} e^x\).
- Zeichne \(K_f\) für \(-3\leq x\leq 3\) in ein Koordinatensystem ein.
- Berechne die Gleichung der Tangente \(t\) in der Nullstelle der Funktion.
- Begründe, dass die Gerade \(g\) mit \(y=4\) keine Tangente an die Kurve \(K_f\) ist.
- Zeige: Alle Tangenten an \(K_f\) haben negative Steigung.
| AFB II - K1 K4 K5 | Quelle Dirk Tebbe, Martin Stern |
3 Tangente in einem Kurvenpunkt III (k.A.) 𝕃
Eine Schülerin findet in ihren Unterlagen den nachfolgend abgebildeten Aufschrieb zu einer gelösten Aufgabe. Leider ist die dazu gehörende Aufgabenstellung verlorengegangen.
Hilf der Schülerin und erstelle eine zur Lösung passende Aufgabenstellung.
- 1.
\(h(x)=cos(\frac{\pi}{4}x)+1\)
\(h'(x)=\frac{\pi}{4}\cdot (-sin(\frac{\pi}{4}x))+1=-\frac{\pi}{4} sin(\frac{\pi}{4}x)\)
\(h'(6)=-\frac{\pi}{4}sin(\frac{\pi}{4}\cdot 6)=\frac{\pi}{4}\)
\(h(6)=1\)
Einsetzen von \(m=\frac{\pi}{4}\) und \(P(6|1)\)in \(y=mx+c\) liefert \(c=1-\frac{3}{2}\pi\).
\(t: y=\frac{\pi}{4}x+1-\frac{3}{2}\pi\) \(h'(x)=m\)
\(-\frac{\pi}{4} sin(\frac{\pi}{4}x)=2\)
\(sin(\frac{\pi}{4}x)=-\frac{8}{\pi}\)
Substituiere:\(\frac{\pi}{4}x=u\)
\(sin(u)=-\frac{8}{\pi}\)
\(-\frac{8}{\pi}<-1\)
\(-\frac{8}{\pi}\) liegt somit ausserhalb des Wertebereichs der Sinusfunktion.
Deswegen hat die Gleichung keine Lösung.
| AFB k.A. - K1 K2 K4 K5 | Quelle Dirk Tebbe, Martin Stern |
4 Polynomfunktionen (5 min) 𝕃
Zeige, dass für alle Polynomfunktionen f der Form \(f(x)=a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0\) gilt, dass \(a_1 x + a_0\) eine Tangente an den Graphen an der Stelle x = 0 ist.
| AFB II - K5 | Quelle Holger Engels |
5 Tangente und Schnittpunkt (k.A.) 𝕃
Gegeben ist die in \(\mathbb{R}\) definierte Funktion \(f\) mit \(f\left(x\right)=\frac{1}{2}\cdot x^2\).
Die Abbildung zeigt den Graphen von \(f\) sowie die Tangente \(t\) an den Graphen von \(f\) im Punkt \(\left(4\middle| f\left(4\right)\right)\).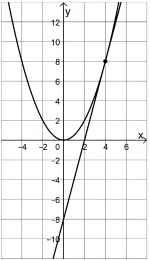
- Gib anhand der Abbildung eine Gleichung der Tangenten \(t\) an.
- Weise nach, dass für jeden Wert \(u\in\mathbb{R}\) die Tangente an den Graphen von \(f\) im Punkt \(\left(u\middle| f\left(u\right)\right)\) die y-Achse im Punkt \(\left(0\middle|-f\left(u\right)\right)\) schneidet.
| AFB k.A. - K1 K2 K4 K5 | Quelle IQB e.V. | #iqb |
6 Funktion gesucht (11 min) 𝕃
Bestimme einen Funktionsterm, dessen Graph an der Stelle x = 2 die Tangente \(g(x)=\frac12 x+1\) hat.
| AFB III - K2 K5 | Quelle Holger Engels | #problemlösen |
