1 Uneigentliches Integral (40 min) 𝕃
Betrachtet wird für negative rationale Zahlen q die Potenzfunktion p mit \(p(x)=x^q;\: x\neq 0\).
Für \(b \rightarrow \infty\) heißt \(U_q=\int_1^b{p(x)}\cdot dx\) uneigentliches Integral über p, falls \(U_q\) eine reelle Zahl ergibt.
Überprüfe, für welche Werte von q das uneigentliche Integral \(U_q\) existiert.

| AFB III - K2 K5 | Quelle Dr. Andreas Dinh | #problemlösen |
2 Annäherung (30 min) 𝕃
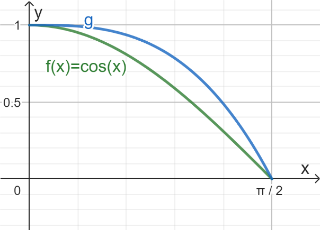 In \([0; \pi/2]\) soll die Funktion f mit \(f(x)=\cos{x}\) durch eine Potenzfunktion g mit \(g(x)=1-ax^q\) angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.
In \([0; \pi/2]\) soll die Funktion f mit \(f(x)=\cos{x}\) durch eine Potenzfunktion g mit \(g(x)=1-ax^q\) angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.
- Bestimme a in Abhängigkeit von q.
Begründe, weshalb ein kleiner Wert des Integrals
\[\int_0^{\frac{\pi}{2}} f(x)-g(x)\cdot dx\]ein guter Hinweis dafür ist, dass g eine gute Näherung für f ist.
- Finde eine Potenzfunktion g, die f gemäß des Kriteriums von b) gut annähert.
(Bonus: Stelle f und die Annäherung aus c) mit Geogebra dar und berechne die durchschnittliche Abweichung von f und der Annäherungsfunktion.)
| AFB III - K2 K5 K4 | Quelle Dr. Andreas Dinh | #problemlösen |
3 Steigung, Volumen (k.A.) 𝕃
Die Abbildung zeigt den Graphen einer in \(\mathbb{R}\) definierten Funktion \(f\).
- Beurteile die folgende Aussage:
Für jeden Wert von \(x\) mit \(0\leq x\leq 2\) ist die Steigung des Graphen von \(f\) kleiner als 3. - Mit dem Term \(\pi\cdot\int\limits_{0}^{2}{\left(f\left(x\right)\right)^2\mathrm{d} x}\)
kann das Volumen eines Körpers berechnet werden.
Begründe, dass dieses Volumen größer als \(\pi\cdot{0,5}^2+\pi\cdot1^2\) ist.
| AFB k.A. - K1 K2 K4 K5 K6 | Quelle IQB | #iqb |
