Zum Inhalt springen

Lösung Annäherung

Version 4.1 von akukin am 2023/11/12 15:46

cos und pot.png a) a wird in Abhängigkeit von q so gewählt, dass \( \frac{\pi}{2}\)  eine Nullstelle von g ist: 

\( g\bigl(\frac{\pi}{2}\bigl)=0 \Leftrightarrow 1 - a \bigl(\frac{\pi}{2}\bigl)^q=0\).

Auflösen nach a ergibt:

\( a \cdot \bigl(\frac{\pi}{2}\bigl)^q=1 \Leftrightarrow a = \frac{1}{\bigl(\frac{\pi}{2}\bigl)^q}=\bigl(\frac{\pi}{2}\bigl)^{-q}=\bigl(\frac{2}{\pi}\bigl)^q\).

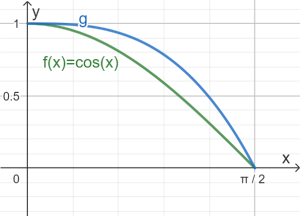
b) Idee: Wenn f und g wie im Beispiel der Zeichnung keine Schnittpunkte in \(]0;\frac{\pi}{2}[\) haben, dann ist ein kleiner Flächeninhalt zwischen den Graphen ein gutes Maß für eine kleine Abweichung zwischen den Graphen.
Wenn f und g hingegen einen oder mehrere Schnittpunkte in \(]0;\frac{\pi}{2}[\) haben, dann müssen aufgrund der Schnittpunkte bei 0 und π/2 und aufgrund der Rechtskrümmung beider Graphen die Teilflächen zwischen den Kurven klein sein und auch dann liegt eine gute Annäherung vor.

c) Das Integral muss in Abhängigkeit von q ausgerechnet werden und soll dann möglichst klein sein:

\[ \begin{align} & \int_0^{\pi/2}f(x)-g(x)dx \\ &= \int_0^{\pi/2}\cos(x)-1+ \Bigl(\frac{2}{\pi}\Bigl)^q x^q dx\\ &= \int_0^{\pi/2}\cos(x)+ \Bigl(\frac{2}{\pi}\cdot x \Bigl)^q - 1 dx\\ &= \Bigl[\sin(x) + \frac{\frac{\pi}{2}}{q+1}\Bigl(\frac{2}{\pi}x\Bigl)^{q+1}-x\Bigl]_0^{\frac{\pi}{2}} \\ &= \sin\Bigl(\frac{\pi}{2}\Bigl) + \frac{\frac{\pi}{2}}{q+1}\cdot 1^{q+1}- \frac{\pi}{2}-(\sin(0) + \frac{\frac{\pi}{2}}{q+1} \cdot 0^{q+1}-0) \\ &= 1 +\frac{\frac{\pi}{2}}{q+1} - \frac{\pi}{2} \\ &= 1 + \frac{\pi}{2} \Bigl(\frac{1}{q+1}-1 \Bigl) \end{align}\]

Nullsetzen und Auflösen oder Wertetabelle mit WRT führt zu einer Nullstelle bei \( q= \frac{1}{1-\frac{2}{\pi}} -1 \approx 1,751 \).
Für dieses q ist das Integral also gleich Null.

Bonus:
[Bonusplot.png||width="300"]]

Schnittstelle laut Geogebra: \( x_S \approx 0,87018353\)

\(\Bigl| \int_0^{0,78018353} f(x)-g(x) dx \Bigl| \approx 0,0066166 \Rightarrow A_{ges} = 0,01323321\) 

Es folgt eine durchschnittliche Abweichung von \( \frac{A_{ges}}{\pi/2} \approx 0,0084245\)