Lösung Sinusgraph
Zuletzt geändert von akukin am 2025/08/14 17:20
Teilaufgabe 1
Erwartungshorizont
Der Graph \(G_f\), die x-Achse sowie die Geraden mit den Gleichungen \(x=-2\) und \(x=8\) schließen eine Fläche ein, deren Teil unterhalb der x-Achse einen kleineren Inhalt besitzt als deren Teil oberhalb. Deshalb ist der Wert des Integrals nicht negativ.Erläuterung der Lösung
Für beide Teilflächen unterhalb der x-Achse gibt es symmetrisch zur jeweiligen Nullstelle eine gleichgroße Teilfläche oberhalb der x-Achse (rot und blau). Die grüne Teilfläche bleibt übrig und zählt positiv zum Integral.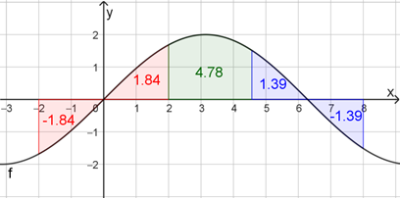
Die Aufgabe könnte auch rechnerisch gelöst werden:
\[\begin{align*}
\int_{-2}^{8}{2\cdot\sin{\left(\frac{1}{2}x\right)}\mathrm{d} x}&=\left[-4\cdot\cos{\left(\frac{1}{2}x\right)}\right]_{-2}^8 \\
&=-4\cdot\cos{\left(4\right)}-\left(-4\cdot\cos{\left(-1\right)}\right) \\
&=-4\cdot\cos{\left(4\right)}+4\cdot\cos{\left(-1\right)}
\end{align*}\]
Jedoch ist das Vorzeichen dieses Rechenergebnisses ohne Taschenrechner nur schwer zu ermitteln.Teilaufgabe 2
Erwartungshorizont
Wegen \(f^\prime\left(x\right)=\cos{\left(\frac{1}{2}x\right)}, f^\prime\left(0\right)=1\) und \(f\left(0\right)=0\) besitzt die Tangente an \(G_f\) im Koordinatenursprung die Gleichung \(y=x\), die auch die Gerade durch die beiden gegebenen Punkte beschreibt.Erläuterung der Lösung
Die Tangentengleichung kann mit folgender Formel ermittelt werden:\(y=f^\prime\left(u\right)\cdot\left(x-u\right)+f\left(u\right)\)
wobei \(x=u\) diejenige Stelle ist, an der die Tangente am Graphen anliegt.
Da in unserem Fall die Tangente durch den Ursprung gehen soll, ist \(u=0\) und \(f\left(u\right)=0\):
\(y=f^\prime\left(0\right)\cdot x\)
Wir benötigen also nur noch \(f^\prime\left(0\right)\):
\(f\left(x\right)=2\cdot\sin{\left(\frac{1}{2}x\right)}\ \ \Rightarrow\ f^\prime\left(x\right)=\cos{\left(\frac{1}{2}x\right)}\)
\(f^\prime\left(0\right)=\cos{\left(0\right)}=1\)
Folglich lautet die Gleichung der Tangente:
\(y=x\)
Zwei Punktproben mit den Punkten \(\left(-1\middle|-1\right)\) und \(\left(1\middle|1\right)\) liefern wahre Aussagen, das heißt die Punkte liegen auf der Tangente.
