Zum Inhalt springen

Lösung Quadrat Diagonale

Zuletzt geändert von akukin am 2024/10/19 11:20
Erwartungshorizont \(\left(\begin{array}{c} -1 \\ 4 \\ -2 \end{array}\right)+\lambda\cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right)=\left(\begin{array}{c} x_1 \\ x_2 \\ 0 \end{array}\right)\) liefert \(\lambda=2\).
Schnittpunkt \(M\) der Diagonalen: \(M\left(3\left|4\right|0\right)\)
\(\left|\overrightarrow{OM}\right|=\sqrt{3^2+4^2}=5\)
Flächeninhalt des Quadrats: \(4\cdot\frac{1}{2}\cdot5^2=50\)
Erläuterung der Lösung 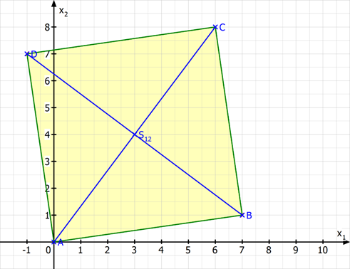Quadrateingezeichnet.png Da der Schnittpunkt der Diagonalen \(S_{12}\) in der x1x2-Ebene liegt, muss die x3-Koordinate null sein. Der gesuchte Punkt auf der Geraden kann also mit \(S_{12}\left(x_1\left|x_2\right|0\right)\) beschrieben werden.
Die Gleichung der Geraden ist \(g: \ \vec{x}=\left(\begin{array}{c} -1 \\ 4 \\ -2 \end{array}\right)+\lambda\cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right) \) mit \(\lambda\in\mathbb{R}\).
Setzen wir diese mit dem Ortsvektor von \(S_{12}\) gleich, erhalten wir den Wert des Parameters \(\lambda\) und damit die beiden fehlenden Koordinaten von \(S_{12}\):
\(\left(\begin{array}{c} -1 \\ 4 \\ -2 \end{array}\right)+\lambda\cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right)=\left(\begin{array}{c} x_1 \\ x_2 \\ 0 \end{array}\right)\)
Da die x3-Koordinate null sein muss, ist \(\lambda=2\). Setzt man \(\lambda=2 \) in die Geradengleichung ein \(\left(\begin{array}{c} -1 \\ 4 \\ -2 \end{array}\right)+2 \cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right)=\left(\begin{array}{c} -1+2\cdot 2 \\ 4+2\cdot 0 \\ -2+2\cdot 1 \end{array}\right)=\left(\begin{array}{c} 3\\ 4 \\ 0 \end{array}\right)\)

erhält man \(S_{12}\left(3\left|4\right|0\right)\).

Die Fläche des Quadrats besteht aus vier gleichgroßen rechtwinkligen Dreiecken, deren Katheten jeweils die Länge \(\left|\overrightarrow{OS_{12}}\right|\) haben (die Hälfte der gleichlangen Diagonalen).

\(\left|\overrightarrow{OS_{12}}\right|=\sqrt{3^2+4^2}=5\)

Also ist der Flächeninhalt des Quadrats:
\(A_{\mathrm{Quadrat}}=4\cdot A_{\mathrm{Dreieck}}=4\cdot\left(\frac{1}{2}\cdot5\cdot5\right)=50\)