Hinweise und Lösungshilfen
Hinweis Teilaufgabe a)
Bei der Zufallsgröße \(Y\) wird als Treffer gezählt, was bei der Zufallsgröße \(X\) den Nicht-Treffer darstellt und umgekehrt.
Folglich können Symmetrieeigenschaften verwendet werden, um die Wahrscheinlichkeitsverteilung von \(Y\) zu zeichnen.
Hinweis Teilaufgabe b)
Damit die Wahrscheinlichkeitsverteilungen der beiden binomialverteilten Zufallsgrößen \(X\) und \(Z\) identisch sein können, müssen die Parameter \(n\) und \(p\) gleich sein.
Hinweis Teilaufgabe c)
Der Parameter \(n=4\) ist bei beiden Zufallsgrößen bereits gleich.
Wie kann \(Z\) formuliert werden, damit auch die Trefferwahrscheinlichkeiten \(p\) identisch sind?
Lösung:
Erläuterung:
Bei der Zufallsgröße \(Y\) wird als Treffer gezählt, was bei der Zufallsgröße \(X\) als Nicht-Treffer gezählt wird und umgekehrt.
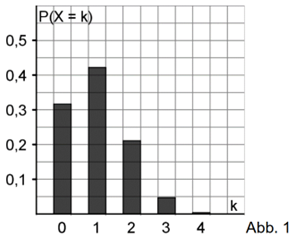
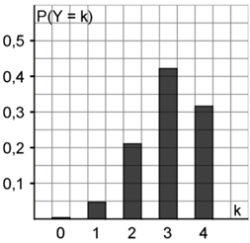
Es gilt also: \(P(Y=0)=P(X=4); \ P(Y=1)=P(X=3); \ P(Y=2)=P(X=2)\) usw.
Folglich kann die Wahrscheinlichkeitsverteilung von \(X\) an der vertikalen Geraden durch \(k=2\) gespiegelt werden, um die Wahrscheinlichkeitsverteilung von \(Y\) zu erhalten.
2. \(Z\): Anzahl der Würfe, bei denen keine der beiden erzielten Zahlen größer als drei ist.
Erläuterung:
Wir benötigen eine Zufallsgröße \(Z\) mit \(n=4\) und \(p=\frac{1}{4}\), denn das sind die Parameter von \(X\).
\(n=4\) ist bei \(Z\) schon vorausgesetzt (siehe Aufgabenstellung, „viermaliges Werfen“).
Zu überlegen ist also, wie man einen Treffer festlegt, dessen Trefferwahrscheinlichkeit \(p=\frac{1}{4}\) beträgt. Da die beiden Würfel farblich unterscheidbar sind, ist das einmalige Würfeln mit beiden Würfeln ein Laplace-Experiment, denn wenn beispielsweise das Ergebnis \(14\) bedeutet, dass der rote Würfel eine \(1\) zeigt und der grüne Würfel eine \(4\), dann lautet die Ergebnismenge
\(S={11,12,13,…,21,22,23,…65,66}\)
und jedes darin enthaltene Ergebnis ist gleich wahrscheinlich.
Diese Ergebnismenge enthält \(6^2=36\) Ergebnisse, also müssen wir als Treffer ein Ereignis festlegen, das \(9\) Ergebnisse enthält, damit wir auf \(p=\frac{9}{36}=\frac{1}{4}\) kommen.
Das Ereignis „Keine der beiden Zahlen ist größer als \(3\)“ beinhaltet tatsächlich \(9\) Ergebnisse:
\(E={11,12,13,21,22,23,31,32,33}\)
Also können wir das Treffer-Ereignis festlegen als „Keine der beiden Zahlen ist größer als \(3\)“.
