Lösung Trapez

Ein Trapez ist ein besonderes Viereck mit zwei parallelen Seiten, welche den Abstand \( h\) voneinander besitzen. Die längere der parallelen Seiten soll mit \( a \), die kürzere mit \( c \) bezeichnet werden.

1. Beschrifte das Trapez gemäß der obigen Angaben mit den Parametern \( a \),\( c \) und\( h \).
   
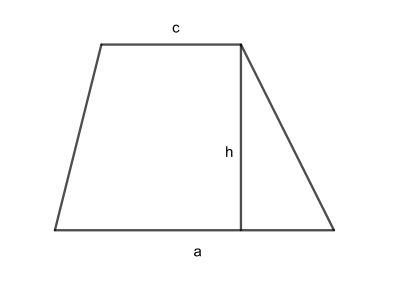
2. Der Flächeninahlt \( A \) des Trapezes kann berechnet werden, indem man die Hälfte der Summe aus den beiden parallelen Seiten mit dem Abstand der beiden parallelen Seiten multipliziert. Stelle diese Formel für \( A \) auf.
   \( A = \frac{a+c}{2} \cdot h = \frac {1}{2} \cdot (a+c) \cdot h \)
3. Überprüfe, ob man die Höhe h mit der Formel \( 2 \cdot \frac{A}{a+c} \) berechnen kann.
   \( A = \frac{a+c}{2} \cdot h \quad | \cdot 2 \)
   \( 2\cdot A =(a+c) \cdot h \)
4. Forme die Formel für den Flächeninhalt des Trapezes mit Hilfe von Äquivalenzumformungen nach der längeren Seite um.
   \( A = \frac{a+c}{2} \cdot h \)
   \( \frac{2 \cdot A}{h} = a+c \)
   \( \frac{2 \cdot A}{h}- c = a \)