BPE 3 Einheitsübergreifend
1 Wertetabellen prüfen (10 min) 𝕃
Beurteile, ob folgende Zuordnungen eine lineare Funktion darstellen. Begründe deine Antwort.
Zusatz (aus BPE 3.5): Gib – wenn möglich – die Funktionsgleichung an.
\(x\) 0 1 2 3 4 5 \(f(x)\) 1,5 3 4,5 6 7,5 9 \(x\) -2 -1 0 1 2 3 \(g(x)\) 4,5 2 -0,5 -3 -5,5 -8 \(x\) 0 3 4 10 12 13 \(h(x)\) 2,5 7 8,5 17,5 20,5 22 \(x\) 0 2 4 6 8 10 \(i(x)\) 0 4 16 36 64 100 \(x\) 0 1 4 6 8 11 \(j(x)\) 40 35 20 10 0 -15 \(x\) -2 0 1 3 7 15 \(k(x)\) 1 0 -0,5 -1,5 -3,5 -7,5 \(x\) -4 -1 1 3 6 7 \(l(x)\) 69 3 9 55 199 267
| AFB II - K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
2 Schnittpunkt zweier Geraden (15 min) 𝕃
 Die Abbildung zeigt zwei Geraden, die sich schneiden.
Die Abbildung zeigt zwei Geraden, die sich schneiden.
- Lies den Schnittpunkt aus der Abbildung möglichst genau ab.
- Ermittle die Geradengleichungen.
- Berechnen den Schnittpunkt exakt.
- Vergleiche die Ergebnisse aus a) und c).
| AFB II - K4 K5 K6 | Quelle kickoff |
3 Zuordnungsaufgabe Funktionsterm und Schaubild (7 min) 𝕃
Ordne den Schaubildern zu:
a) \(y=-\frac{3}{4}x+2\) b) \(y=\frac{1}{3}x\) c) \(y=-\frac{4}{3}x+2\) d) \(y=3x\)
1) 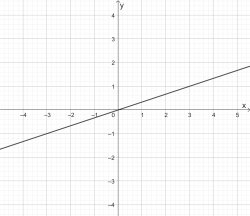 | 2)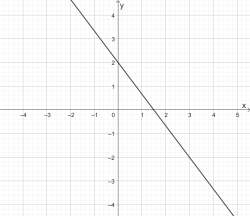 |
3) 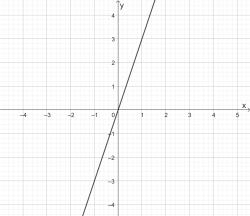 | 4) 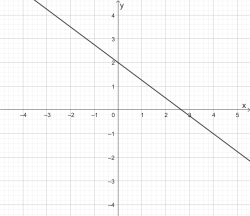 |
| AFB II - K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
4 Geradengleichungen bestimmen (11 min) 𝕃
- Bestimme die Gleichungen der beiden Geraden.
- Bestimme die Schnittpunkte der beiden Geraden mit der x-Achse.
- Gib die Koordinaten des Punktes an, in dem sich die beiden Geraden schneiden.
| AFB II - K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
5 Einkommenssteuer 2025 (10 min)
Beträgt das zu versteuernde Jahreseinkommen mehr als 68 480 € und weniger als 27 7826 €, wird die Einkommensteuer (in Euro) berechnet nach der Vorschrift
\( 0,42\cdot x\ –\ 10\ 912\).
Dabei ist \(x\) das zu versteuernde Einkommen.
- Berechne, wie viel Einkommensteuer (in Euro) man bezahlt, wenn das Einkommen 72 882 € beträgt.
- Berechne, wie viel Prozent des Einkommens das sind.
- Berechne, wie viel Steuer man mehr zahlen muss, wenn das Einkommen 100 € höher ist.
Gib an, wieviel Prozent von den 100 € Mehreinkommen das sind. - Beurteile, ob du diesen in c) berechneten „Spitzensteuersatz“ für richtig, für zu hoch oder für zu niedrig hältst.
| AFB I - K1 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
6 Geradenbüschel (11 min) 𝕃
Im obigen Koordinatensystem sind verschiedene Geraden eingezeichnet.
- Nenne eine Gemeinsamkeit aller dieser Geraden.
- Gib zu drei dieser Geraden die zugehörige Gleichung an.
- Gib an, wie die Gleichung der Parallelen zur x-Achse bzw. zur y-Achse in diesem Bündel lautet.
- Beurteile, welche der beiden Gleichungen aus c) keine Funktion beschreibt.
| AFB II - K1 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
7 Handykosten (16 min) 𝕃
Ein Handynetzbetreiber wirbt für folgenden Handytarif
| Die ersten 6 Minuten für 4 Cent je Minute telefonieren, danach für 2 Cent je Minute. |
a) Überprüfe, welche der nachfolgenden Wertetabellen diesen Tarif beschreibt.
Tabelle 1
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 4 | 4 | 4 | 4 | 4 | 2 | 2 | 2 | 2 |
Tabelle 2
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 8 | 12 | 16 | 20 | 24 | 26 | 28 | 30 | 32 |
Tabelle 3
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 8 | 12 | 16 | 20 | 24 | 38 | 40 | 42 | 44 |
Richtig ist Tabelle .
Ein Konkurrent wirbt hingegen für folgenden Tarif
| Die ersten 4 Minuten für 5 Cent je Minute telefonieren, danach für 2 Cent je Minute. |
b) Erstelle eine Wertetabelle für die ersten 10 Gesprächsminuten dieses Handytarifs.
c) Zeichne ein Schaubild, das die Kosten in Cent in Abhängigkeit von den telefonierten Minuten darstellt.
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
8 Paddelboottour (17 min) 𝕃
Lisa und ihre Eltern möchten im Spreewald eine Paddelboottour machen.
Sie stehen folgender Informationstafel gegenüber:
Leihgebühr 7,00 € + jede Minute 0,10 €
Keine Leihgebühr, jede Minute kostet 0,30 €
Pauschalpreis für 90 Minuten 15,00 €.
Jede darüber hinausgehende Minute kostet 0,50 €.
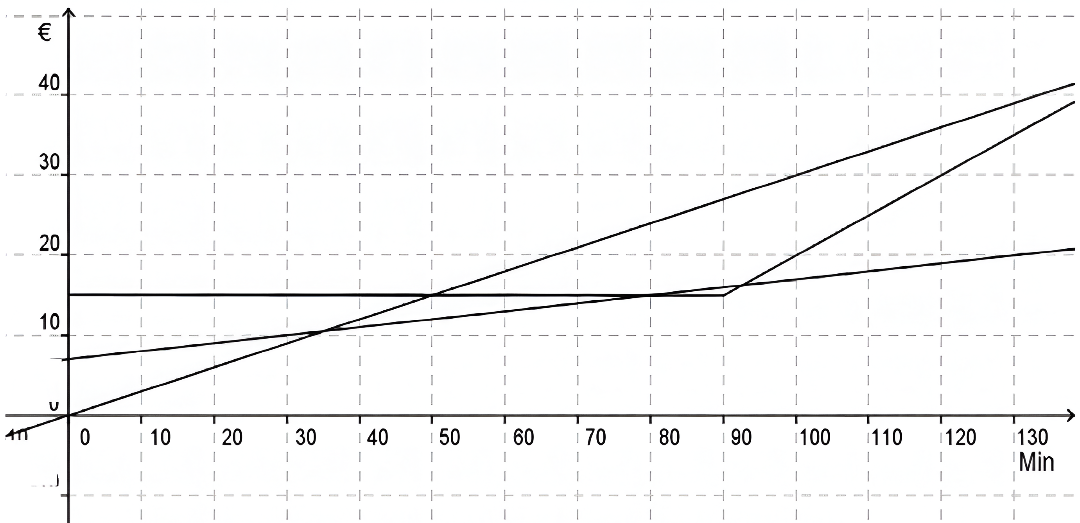
- Ordne die Schaubilder den Angeboten zu.
- Bestimme, welches Angebot die Familie nutzen soll, wenn die Familienmitglieder 30 Minuten fahren möchten und sie möglichst wenig dafür ausgeben möchten.
- Der Vater ist bereit, 25,00 € für die Paddelboottour auszugeben. Ermittle das Angebot, mit dem Familie möglichst lange fahren kann. Berechne, wie lange sie bei diesem Angebot fahren können.
- Beurteile, ob es eine Fahrtdauer gibt, bei der es egal ist, welches Angebot gewählt wird.
| AFB II - K1 K3 K4 K5K6 | Quelle Team Mathebrücke | #mathebrücke |
9 Handytarife Schaubildern zuordnen (9 min) 𝕃
a) Ordne den folgenden Tarifen je ein Schaubild zu
Keine Grundgebühr und ganztags nur 0,50 €/Min. in alle Netze!
Superflat für 25,00 €!
Grundgebühr 10 €, ganztags 0,30 €/Min. in alle Netze! Die ersten 50 Minuten sind inklusive!
Grundgebühr 10 €, ganztags 0,30 €/Min. in alle Netze!
Grundgebühr 20 €, ganztags 0,20 €/Min. in alle Netze!
b) Gib die Geradengleichungen zu den einzelnen Handytarifen an.
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
10 Akkuentladung (9 min) 𝕃
Kevin hat ein Handy mit einem Akku, der sich im Ruhezustand innerhalb von 14 Tagen gleichmäßig entleert. Wenn der Akku voll geladen ist, enthält er 200 mAh elektrische Ladung.
- Stelle die Entladung des Akkus in 14 Tagen in einem Schaubild dar.
- Bestimme, wie viel Ladung der Akku nach 9 Tagen enthält.
- Berechne, nach wie vielen Tagen 80 Prozent der Ladung weg sind.
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
11 Mietwagenpreise (7 min) 𝕃
Frau Martin hat sich einen Mietwagen genommen und ist damit 140 Kilometer gefahren. Sie erhält eine Rechnung über 124,00 Euro. Dieser Wert beinhaltet eine Tagespauschale und einen Kilometerpreis. Herr Martin mietet denselben Wagen am nächsten Tag und fährt damit 80 km. Er muss 88 Euro bezahlen. Die Tochter der Familie Martin hatte sich den Wagen auch schon einmal für 180,00 Euro gemietet. Sie fuhr 200 km. Sie vergleicht ihre Kosten mit den Rechnungen ihrer Eltern. Beurteile, ob sie zu Recht verärgert ist
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
12 Richtig-Falsch-Aufgabe zu Schaubildern linearer Funktionen (10 min) 𝕃
Kreuze jeweils an, ob die Aussage richtig oder falsch ist.
Formuliere die falschen Aussagen zu einer richtigen Aussage um.
- Gerade a hat die Steigung \(\frac{1}{3}\).
☐ richtig ☐ falsch - Der y-Achsenabschnitt der Geraden c beträgt 3,5.
☐ richtig ☐ falsch - Die Gerade b hat die Steigung 1.
☐ richtig ☐ falsch - Die Geraden a und b schneiden sich im Punkt \(S\left(-\frac{33}{8}\Bigl|\frac{17}{8}\right)\)
☐ richtig ☐ falsch - Die Geraden c und e schneiden sich nie.
☐ richtig ☐ falsch - Die Gerade e hat die Gleichung \(y=3\).
☐ richtig ☐ falsch - Die Gerade d ist das Schaubild einer Funktion, da jedem x-Wert genau ein y-Wert zugeordnet wird.
☐ richtig ☐ falsch - Die Geraden b und e schneiden sich im Punkt \(S(3|-5,5)\)
☐ richtig ☐ falsch - Die Geraden a und f unterscheiden sich nur durch ihren y-Achsenabschnitt.
☐ richtig ☐ falsch - Eine Gerade, die orthogonal (senkrecht) auf der Geraden c stehen würde, hätte die Steigung \(\frac{1}{3}\).
☐ richtig ☐ falsch
| AFB II - K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
13 Selbst Beispiele geben (10 min) 𝕃
Betrachte die Funktion f mit \(f(x)=-\frac{1}{4}x+1\)
- Überprüfe, ob der Punkt \(P(2|0,5)\) auf dem Schaubild liegt.
- Gib je einen Punkt an, der oberhalb bzw. unterhalb der Geraden liegt.
- Gib eine lineare Funktion g an, deren zugehöriges Schaubild das Schaubild von f nicht schneidet.
- Gib eine lineare Funktion h an, deren Schaubild das Schaubild von f im Punkt \(P(1|0,75)\) schneidet.
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
14 Geradengleichungen (10 min) 𝕃
Gegeben sind die Gerade \(g_1: y=-2x+4\) sowie die Punkte \(A(1|2)\) und \(B(4|3)\).
- Zeige, dass der Punkt A auf der Geraden g1 liegt.
- Bestimme die Gleichung einer Geraden g2 durch die Punkte \(A(1|2)\) und \(B(4|3)\).
- Berechne die Koordinaten des Schnittpunkts von g1 und g2. Gib an, welcher Punkt sich dabei ergeben muss.
| AFB II - K5 | Quelle Team Mathebrücke | #mathebrücke |
15 Zusammenhang Masse und Volumen (10 min) 𝕃
Vergleicht man Stoffe mit dem gleichen Volumen, so besitzen diese meist unterschiedliche Massen. Der Zusammenhang zwischen Masse und Volumen für verschiedene Stoffe wird in folgendem Diagramm dargestellt:
- Die Stoffe besitzen jeweils ein Volumen von 300 cm3. Bestimme die Masse des jeweiligen Stoffs.
- Berechne, bei welchem Volumen Magnesium die gleiche Masse besitzt wie 300 cm3 Wasser.
- Bestimme jeweils eine zugehörige Geradengleichung.
| AFB II - K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
16 Aufgabe zu Funktionsvorschriften (10 min) 𝕃
Gegeben sind die Funktionen \(f\) mit \(f(x) = \frac{1}{8}x - \frac{3}{2}\) und \(g\) mit \(g(x) = -\frac{1}{2}x + \frac{7}{8}\).
- Bestimme den Wert von \(x\), wenn gilt: \(f(x) = -\frac{5}{8}\)
- Berechne den Wert von \(x\), wenn gilt: \(f(7) = g(x)\)?
- Ermittle den Wert von \(c\), wenn gilt: \(f(5) + c = g(6)\).
| AFB III - K5 | Quelle Team Mathebrücke | #mathebrücke |
17 Richtig-Falsch-Aufgaben zu Funktionsvorschriften (10 min) 𝕃
Gegeben sind die Funktionen \(f\) durch \(f(x) = -3x+7\) und \(g\) durch \(g(x) = \frac{1}{3}x-2\).
Kreuze jeweils an, ob die Aussage richtig oder falsch ist.
Formuliere die falschen Aussagen zu einer richtigen Aussage um.
- Die Funktion \(f\) nimmt an der Stelle 3 den Funktionswert 1 an.
☐ richtig ☐ falsch - Es gilt \(g(9) = 1\).
☐ richtig ☐ falsch - Das Schaubild der Funktion \(f\) schneidet die x-Achse an der Stelle \(\frac{7}{3}\).
☐ richtig ☐ falsch - Die Funktionen \(f\) und \(g\) nehmen an der Stelle \(x = 2,5\) denselben Funktionswert an.
☐ richtig ☐ falsch - Die Schaubilder der Funktionen stehen senkrecht aufeinander.
☐ richtig ☐ falsch - Die Funktion \(f\) ordnet dem Wert 5 eine kleinere Zahl zu als die Funktion \(g\).
☐ richtig ☐ falsch - Die Funktion \(g\) ordnet allen Werten größer 6 negative Funktionswerte zu.
☐ richtig ☐ falsch
| AFB III - K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
18 Länge und Mittelpunkt einer Strecke (10 min) 𝕃
In nachfolgendem Koordinatensystem sind mehrere Punkte eingezeichnet.
- Bestimme die Länge der Strecken \(BE\) und \(BD\).
- Gib die Koordinaten des Mittelpunktes \(M\) der Strecke \(EA\) an.
Überprüfe, ob die Gerade durch den Punkt \(D\) mit Steigung -1 durch \(M\) geht. - Berechne den Umfang des Dreiecks \(BAC\).
| AFB III - K5 | Quelle Team Mathebrücke | #mathebrücke |
19 Länge und Mittelpunkt einer Strecke 2 (8 min) 𝕃
- Berechne die fehlenden Koordinaten, wenn \(M\) der Mittelpunkt der Strecke \(P_1P_2\) ist: \(P_1(-3|2); \ \ P_2(0|0);\ \ M( ?|? )\)
\([P_1(4|?); \ \ P_2(-2|5);\ \ M(?|3,5)] \) - Gegeben sind die Punkte \(A(3|-5)\) und \(B(7|2)\). Bestimme die Gleichung der Geraden mit \(m = 0,5\), die durch den Mittelpunkt der Strecke \(AB\) verläuft.
- Zeige, dass die Entfernung des Punktes \(A\) vom Schnittpunkt der Geraden aus b) mit der y-Achse 10 beträgt.
| AFB III - K5 | Quelle Team Mathebrücke | #mathebrücke |
20 Tinas Orthogonale (8 min) 𝕃
Tina hat folgende Hausaufgabe bekommen: Zwei Geraden stehen orthogonal zueinander und schneiden sich im Punkt \(P(-3|-2)\). Bestimmen Sie mögliche Geradengleichungen.
Schau dir an, was sie in ihr Heft notiert hat:
- Erläutere kurz, warum Tina die Steigung \(m = 5\) frei wählen durfte.
- Bestimme für Tina die zugehörige Orthogonale.
| AFB III - K1 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
21 T-Shirtkosten (k.A.) 𝕃
Bei der Produktion von T-Shirts mit aufwendigem Druck und aufgenähten Strasssteinen fallen in einem Unternehmen variable Stückkosten (= Kosten für die Produktion eines T-Shirts) in Höhe von 15 Euro an. Ab einer Menge von 200 T-Shirts betragen die variablen Stückkosten nur noch 11 Euro, da das Unternehmen Einkaufsrabatte nutzen kann.
- Bestimme den Funktionsterm, der die Kosten für eine Produktionsmenge kleiner 200 Stück angibt.
Bestimme auch den Funktionsterm für größere Produktionsmengen. - Zeichne den Kostenverlauf des Unternehmens in Abhängigkeit von der Produktionsmenge in ein Koordinatensystem.
- Erläutere, wie sich das Schaubild verändern würde, wenn in dem Unternehmen fixe Kosten, die unabhängig von der produzierten Menge sind, in Höhe von 600 Euro anfallen würden.
| AFB III - K1 K3 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
22 Fruchtsafttank (10 min) 𝕃
Ein Fruchtsafthersteller nutzt zylinderförmige Edelstahltanks zur Zwischenlagerung von Fruchtsäften. Ein Tank fasst 6000 Liter und wird gleichmäßig gefüllt. Nach 6 Minuten sind 2100 Liter im Tank, eine Viertelstunde später 4350 Liter.
- Stelle die Füllmenge in Abhängigkeit von der Zeit in einem Schaubild dar.
- Bestimme, wie viel Liter zu Beginn noch im Tank waren.
- Berechne, wie lange es dauert, bis der Tank voll ist.
| AFB III - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
23 Geradenbüschel 2 (8 min) 𝕃
Gegeben ist das nebenstehende "Geradenbüschel" (es sind nur 5 von unendlich vielen Geraden eingezeichnet):
- Beschreibe, was diese Geraden gemeinsam haben.
- Beurteile, welche der folgenden Geraden zum Büschel gehören und welche nicht. Begründe deine Antwort.
| Ja | Nein | |
| \(g_1 : y = -7x + 2\) | ☐ | ☐ |
| \(g_2 : y = 2x - 7\) | ☐ | ☐ |
| \(g_3 : y = 2 - 5x\) | ☐ | ☐ |
| \(g_4 : y = 5 - 2x\) | ☐ | ☐ |
| \(g_5 : y = 2\) | ☐ | ☐ |
| \(g_6 : x = 2\) | ☐ | ☐ |
| \(g_7 : 6x + 3y = 2\) | ☐ | ☐ |
| \(g_8 : 3x + 2y = 4\) | ☐ | ☐ |
| \(g_9 : 2x - 3y = 4\) | ☐ | ☐ |
| AFB III - K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
24 Orthogonale Geraden (15 min) 𝕃
Gegeben sind die Gerade \( g_1 : y = \frac{3}{4}x + 2\) sowie der Punkt \(A(7|1)\).
- Zeichne die Gerade \(g_1\) und den Punkt \(A\) in ein Koordinatensystem.
- Bestimme die Gleichung einer zu \(g_1\) orthogonalen (rechtwinkligen) Geraden \(g_2\) durch den Punkt \(A\).
Zeichne \(g_2\) in das Koordinatensystem ein. - Berechne die Koordinaten des Schnittpunkts \(S\) von \(g_1\) und \(g_2\).
- Berechne den Abstand der Punkte \(A\) und \(S\).
- Beschreibe, welche Bedeutung dieser Abstand für die Gerade \(g_1\) und den Punkt \(A\) hat.
| AFB II - K1 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
25 Die Temperatur in den USA (12 min) 𝕃
Antons Freund aus den USA berichtet per Email, wie warm es ist. Da gibt es Temperaturen von 84°, 96°. Anton wundert sich zunächst und erfährt dann, dass in USA die Temperatur nicht nach Celsius (°C) sondern nach Fahrenheit (°F) gemessen werden. Der Zusammenhang zwischen der Celsius- und der Fahrenheitskala ist linear; 0°C sind 32°F, 100°C sind 212° F.
Anton möchte für sich ein Diagramm erstellen, um die Angaben seines Freundes in Grad Celsius umzuwandeln.
- Erstelle eine solches Diagramm und stelle eine Umrechnungsformel auf.
- Beurteile, was für die Verwendung der Fahrenheit-Skala spricht.
| AFB II - K1 K3 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
26 Lösen von linearen Ungleichungen (k.A.) 𝕋 𝕃
Bestimme jeweils grafisch und rechnerisch die Lösungsmenge folgender Ungleichungen:
- \(-2x + 3 < 5\)
- \(3(x + 4) \geq 6\)
- \(5 - 3x > 4(x - 0,5)\)
- \(6 + 3(x - 1) \leq 4(x + 3(x - 1)) - 8x\)
| AFB I - k.A. | Quelle Team Mathebrücke | #mathebrücke |
| K1 | K2 | K3 | K4 | K5 | K6 | |
|---|---|---|---|---|---|---|
| I | 1 | 0 | 0 | 0 | 1 | 1 |
| II | 4 | 0 | 7 | 15 | 16 | 6 |
| III | 2 | 0 | 2 | 4 | 8 | 4 |
