Zum Inhalt springen

Lösung Schnittwinkel von Geraden

Zuletzt geändert von akukin am 2025/06/18 09:40
  1. Zwei Geraden schneiden sich, wenn sie eine unterschiedliche Steigung besitzen. Da die Steigung bei beiden Geraden unterschiedlich ist (\frac{1}{2} und 3), müssen sie sich schneiden.

  2. Für g_1 beträgt der Winkel 26,57° und für g_2 71,57°.
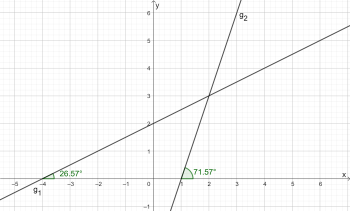
    SchnittwinkelvonGeraden.png

  3. Der Steigungswinkel einer geraden lässt sich berechnen durch \alpha=\tan^{-1}(m)

    Für g_1 ergibt sich: \alpha_1=\tan^{-1}\left(\frac{1}{2}\right)\approx 26,57^\circ

    Für g_2 ergibt sich: \alpha_2=\tan^{-1}\left(3\right)\approx 71,57^\circ

  4. Der Schnittwinkel der beiden Geraden ergibt sich aus der Differenz der beiden Steigungswinkel:
    \alpha_2-\alpha_1=71,57^\circ-26,57^\circ=45^\circ