BPE_8_4
K4 K5 K6 Ich kann den Zusammenhang zwischen den verschiedenen Darstellungsformen von Parabeln durch quadratische Gleichungen erläutern.
K4 Ich kann mithilfe einer Wertetabelle Parabeln zeichnen.
K4 K5 Ich kann grafisch und rechnerisch den Scheitelpunkt und die Achsenschnittpunkte von Parabeln ermitteln.
K4 K5 Ich kann Gleichungen von Parabeln in Scheitel- oder gegebenenfalls Linearfaktorform bestimmen.
1 Scheitelpunkt (k.A.) 𝕃
Begründe, welche der folgenden Behauptungen wahr oder falsch sind.
- Eine nach oben geöffnete Parabel mit dem Scheitelpunkt P(3|4) schneidet die x-Achse nicht.
- Eine nach unten geöffnete Parabel mit dem Scheitelpunkt P(15|30) schneidet die x-Achse zwei Mal.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB I - k.A. | Quelle Team Mathebrücke | #mathebrücke |
2 Abschnittsweise definierte Funktionen (k.A.) 𝕃
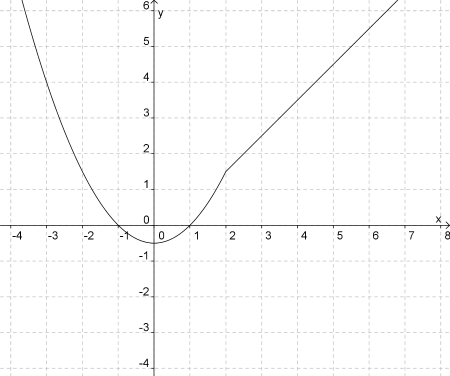
- Lies folgende Funktionswerte ab:
\(f(0) = \)
\(f(3,5) = \)
\(f(-1) = \)
\(f(2) = \) - An welchen Stellen gilt \(y = 4\)?
- Gib die zugehörigen Gleichungen der Funktion an.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II - k.A. | Quelle Team Mathebrücke | #mathebrücke |
3 Darstellungsformen quadratischer Funktionen (3 min)
Die Funktionsgleichung einer quadratischen Funktion kann auf drei verschiedene Arten dargestellt werden:
| Scheitelform | \(f(x)=a\cdot(x-x_S)^2+y_S\) |
| Linearfaktorform | \(f(x)=a\cdot(x-x_1)(x-x_2)\) |
| Hauptform | \(f(x)=ax^2+bx+c\) |
- Gib die Anzahl der unbekannten Parameter an und benenne diese.
- Begründe, warum die Angabe von Scheitel und einem weiteren Punkt zur Aufstellung einer Funktionsgleichung ausreichend ist.
| AFB II - K4 K5 | Quelle S. Hochrein |
4 Verfahrensauswahl (5 min) 𝕃
Je nach Art der gegebenen Informationen ist die Scheitelform oder die Linearfaktorform besonders geeignet zum Aufstellen der Funktionsgleichung.
Begründe jeweils, welche Form bei den im Folgenden gegebenen Informationen zum Aufstellen der Funktionsgleichung geeignet ist.
- Der Graph der Funktion schneidet die x-Achse bei \(-3\) und \(2\) und die y-Achse bei \(-3\).
- Der Scheitel der Funktion liegt bei \(S(2|4)\), der Streckfaktor ist \(a=-2\).
- Der Scheitel liegt bei \(S(3|1)\), der Punkt \(A(5|2)\) liegt auf dem Graphen der Funktion.
- Der Graph der Funktion hat sein Maximum bei \(S(0|2)\), er schneidet die x-Achse bei \(x_1=3\).
Folgende Wertetabelle gehört zur Funktion.
\(x\) 0 1 2 3 4 \(f(x)\) 5 3,5 3 3,5 5 Der Graph der Funktion ist in folgender Abbildung dargestellt.
| AFB II - k.A. | Quelle S. Hochrein |
5 Funktionsterm bestimmen (k.A.) 𝕃
Bestimme die Funktionsterme zur vorangegangenen Aufgabe mit dem jeweils gewählten Verfahren.
| AFB I - k.A. | Quelle S. Hochrein |
