BPE 8.5 Gegenseitige Lage
K4 K5 Ich kann die gegenseitige Lage von Parabeln und Geraden bestimmen.
K5 Ich kann gemeinsame Punkte von Parabeln und Geraden berechnen.
K5 Ich kann gemeinsame Punkte von zwei Parabeln berechnen.
1 Schaubilder zuordnen (5 min) 𝕃
Ordne die drei Schaubilder jeweils den Parabelgleichungen und den Lösungsmengen zu. Begründe deine Entscheidung.
 | keine Schnittpunkte | \(g:y=x^2-2x+2\) \(h:y=2x-2\) | ||
 | zwei Schnittpunkte | \(y=x^2-2x+2\) \(y=-x^2+2x+2\) | ||
 | ein Berührpunkt | \(y=-0,5x^2-4x+1\) \(y=2x^2-3x+2\) |
| AFB I - K1 K4 K5 | Quelle Verena Schmid |
2 Beziehung von Rechnung und Schaubild (25 min) 𝕃
Berechne die Schnittpunkte der Gerade und Parabel. Entscheide anhand des Ergebnisses, wie die Schaubilder zueinander liegen könnten. Skizziere ein mögliches Schaubild. Der Scheitel der Parabel liegt bei S(1/1)
- \(g:y=x^2-2x+2\)
\(h:y=2x-1\) - \(g:y=x^2-2x+2\)
\(h:y=2x-2\) - \(g:y=x^2-2x+2\)
\(h:y=2x-4\)
| AFB I - K1 K2 K4 K5 | Quelle Verena Schmid |
3 Schnittpunktberechnung überprüfen (6 min) 𝕃
Ein Schüler hat die gegenseitige Lage einer Parabel p und einer Geraden g bestimmt. Überprüfe sein Ergebnis.
\(x_{1/2} = \frac{6}{2} \pm \sqrt{\left(\frac{6}{2}\right)^2 - 9} \ \Rightarrow \text{Die Gerade schneidet die Parabel nicht}.\)
| AFB II - K1 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
4 Gerade verschieben (10 min) 𝕋 𝕃
Verschiebe die abgebildete Gerade so, dass sie
- die Parabel schneidet
- die Parabel berührt
- mit der Parabel keinen Punkt gemeinsam hat.
Nenne für jeden der drei Fälle eine Gleichung einer Geraden.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II - K2 K3 K5 | Quelle Team Mathebrücke | #mathebrücke |
5 Parabeln finden (25 min) 𝕃
Gesucht sind Parabeln, die durch den Punkt P gehen und die gegebene Gerade schneiden, berühren oder keinen Punkt mit ihr gemeinsam haben.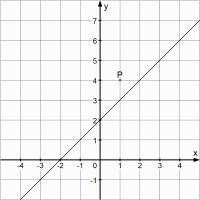
- Beschreibe deine Vorgehensweise.
- Gib zu jedem der drei Fäll die Anzahl der möglichen Parabeln an.
- Bestimme für jeden Fall eine Gleichung einer Parabel. Schildere, wie du deine Ergebnisse überprüfen kannst.
- Hugo behauptet, der Scheitel einer berührenden Parabel läge auf der Geraden. Nimm dazu Stellung.
| AFB III - K2 K3 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
6 Gegenseitige Lage von Parabel und Gerade (8 min) 𝕃
Überprüfe folgende Aussage:
Eine nach unten geöffnete Normalparabel mit dem Scheitel \(S(1|1)\) hat mit der Geraden \(g: y = x + 1\) einen gemeinsamen Schnittpunkt.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB III - K1 K5 | Quelle Team Mathebrücke | #mathebrücke |
7 Gegenseitige Lage von zwei Parabeln (15 min) 𝕃
Gegeben sind folgende Wertetabellen. Sie gehören jeweils zu einer Parabel.
| x | -1 | 0 | 1 | 2 |
| y | 14 | 8 | 6 | 8 |
| x | -1 | 0 | 1 | 2 |
| y | -2 | -1 | 2 | 7 |
Untersuche, wie die Parabeln zueinander liegen.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB III - K2 K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
