Zum Inhalt springen

Pool

Version 15.1 von Holger Engels am 2023/11/03 09:33

10-seitiger Würfel.jpgFünf zehnseitige Würfel (mit den Zahlen 1–10) werden gleichzeitig in einem Würfelbecher geworfen. Für jeden Würfel beträgt die Wahrscheinlichkeit für jede Augenzahl 10%.

Untersuche, wie viele unterschiedliche Wurfbilder geworfen werden können. (unterschiedlich im Sinne von alle verschieden, zwei gleiche, ..., alle gleich)

Bild:  Dietmar Rabich, Würfel, pentagonales Trapezoeder, Ausschnitt, CC BY-SA 4.0

AFB   IIIKompetenzen   k.A.Bearbeitungszeit   k.A.
Quelle   Andreas DinhLizenz   CC BY-SA

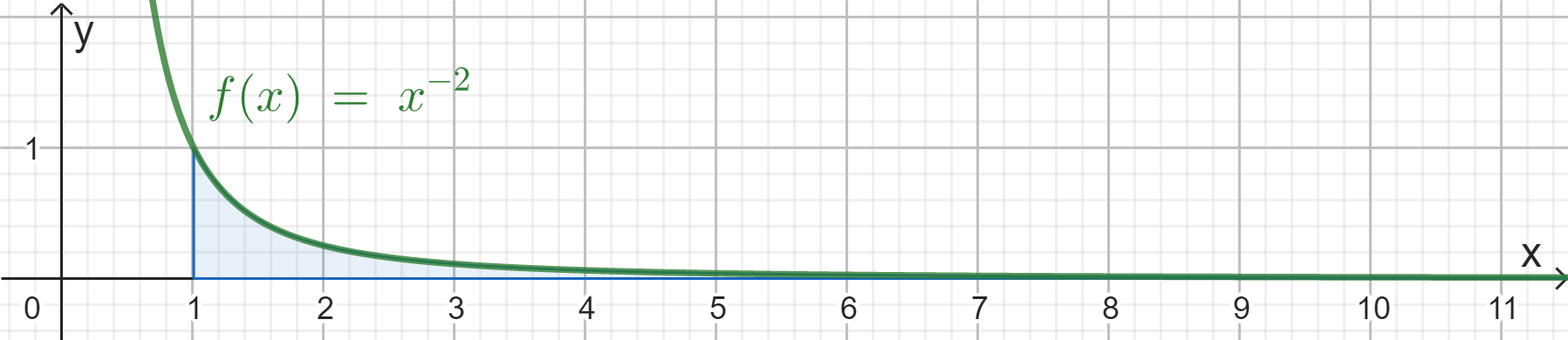
Betrachtet wird für negative rationale Zahlen q die Potenzfunktion p mit p(x)=x^q;\: x\neq 0.

Für b \rightarrow \infty heißt U_q=\int_1^b{p(x)}\cdot dx uneigentliches Integral über p, falls U_q eine reelle Zahl ergibt.

Überprüfe, für welche Werte von q das uneigentliche Integral U_q existiert.

x hoch minus 2.png

AFB   IIIKompetenzen   k.A.Bearbeitungszeit   k.A.
Quelle   Andreas DinhLizenz   CC BY-SA

Glücksrad.svgEin Glücksrad mit einem roten Gewinnbereich von einem Viertel wird so gedreht, dass es in einer völlig zufälligen Position zum Stillstand kommt. Einen Beobachter interessiert, wie groß der Abstand der Halteposition (grünes Dreieck in der Skizze) zum Gewinnbereich ist. Er misst den Abstand in Grad.

So ist der Abstand z.B. 0°, falls das Glücksrad im Gewinnbereich zum Stillstand kommt und 90°, falls es nach einem Drittel oder zwei Dritteln des Verlustbereichs zum Stillstand kommt.

Bestimme mit Hilfe einer geeigneten Zeichnung den Erwartungswert dieses Abstands bei einmaliger Drehung des Glücksrads.

AFB   IIIKompetenzen   k.A.Bearbeitungszeit   k.A.
Quelle   Andreas DinhLizenz   CC BY-SA

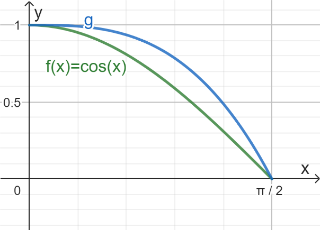cos und pot.pngIn [0; π/2] soll die Funktion f mit f(x)=\cos{x} durch eine Potenzfunktion g mit g(x)=1-ax^q angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.

  1. Bestimme a in Abhängigkeit von q.

  2. Begründe, weshalb ein kleiner Wert des Integrals

    \int_0^{\frac{\pi}{2}} f(x)-g(x)\cdot dx

    ein guter Hinweis dafür ist, dass g eine gute Näherung für f ist.

  3. Finde eine Potenzfunktion g, die f gemäß des Kriteriums von b) gut annähert.

(Bonus: Stelle f und die Annäherung aus c) mit Geogebra dar und berechne die durchschnittliche Abweichung von f und der Annäherungsfunktion.)

AFB   IIIKompetenzen   k.A.Bearbeitungszeit   k.A.
Quelle   Andreas DinhLizenz   CC BY-SA