Pool

Version 25.1 von akukin am 2023/11/07 00:24

Aufgabe 1 Kombinatorik

10-seitiger Würfel.jpg Fünf zehnseitige Würfel (mit den Zahlen 1–10) werden gleichzeitig in einem Würfelbecher geworfen. Für jeden Würfel beträgt die Wahrscheinlichkeit für jede Augenzahl 10%.

Untersuche, wie viele unterschiedliche Wurfbilder geworfen werden können. (unterschiedlich im Sinne von alle verschieden, zwei gleiche, ..., alle gleich)

_{Bild: Dietmar Rabich, Würfel, pentagonales Trapezoeder, Ausschnitt, CC BY-SA 4.0}

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Aufgabe 2 Uneigentliches Integral

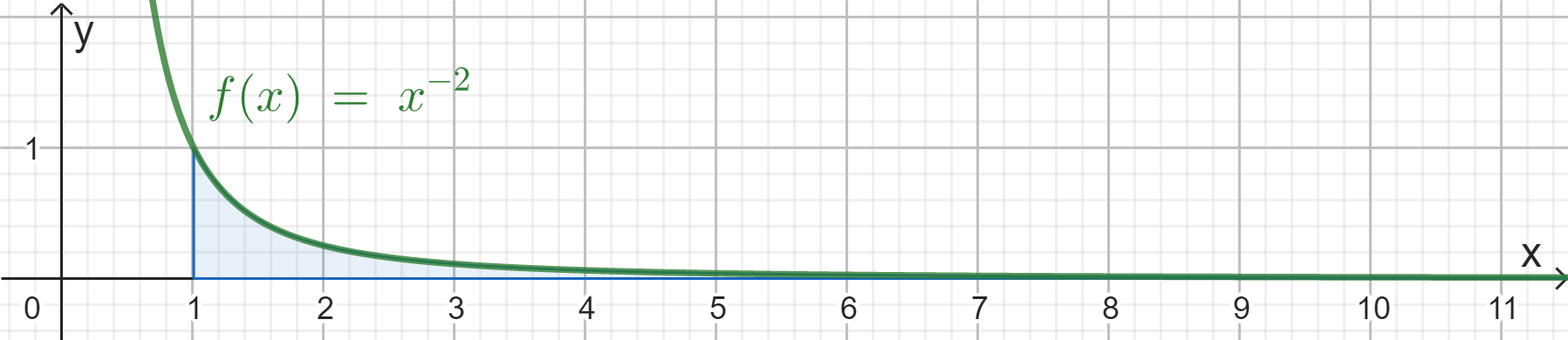
Betrachtet wird für negative rationale Zahlen q die Potenzfunktion p mit $p(x)=x^q;\: x\neq 0$ .

Für $b \rightarrow \infty$ heißt $U_q=\int_1^b{p(x)}\cdot dx$ uneigentliches Integral über p, falls U_q eine reelle Zahl ergibt.

Überprüfe, für welche Werte von q das uneigentliche Integral U_q existiert.

x hoch minus 2.png

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Glücksrad.svg Ein Glücksrad mit einem roten Gewinnbereich von einem Viertel wird so gedreht, dass es in einer völlig zufälligen Position zum Stillstand kommt. Einen Beobachter interessiert, wie groß der Abstand der Halteposition (grünes Dreieck in der Skizze) zum Gewinnbereich ist. Er misst den Abstand in Grad.

So ist der Abstand z.B. 0°, falls das Glücksrad im Gewinnbereich zum Stillstand kommt und 90°, falls es nach einem Drittel oder zwei Dritteln des Verlustbereichs zum Stillstand kommt.

Bestimme mit Hilfe einer geeigneten Zeichnung den Erwartungswert dieses Abstands bei einmaliger Drehung des Glücksrads.

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Aufgabe 4 Annäherung

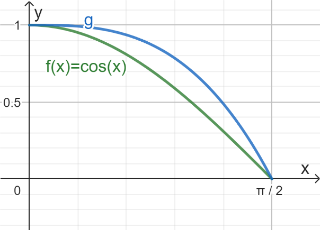cos und pot.png In [0; π/2] soll die Funktion f mit $f(x)=\cos{x}$ durch eine Potenzfunktion g mit g(x)=1-ax^q angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.

Bestimme a in Abhängigkeit von q.
Begründe, weshalb ein kleiner Wert des Integrals
$\int_0^{\frac{\pi}{2}} f(x)-g(x)\cdot dx$
ein guter Hinweis dafür ist, dass g eine gute Näherung für f ist.
Finde eine Potenzfunktion g, die f gemäß des Kriteriums von b) gut annähert.

(Bonus: Stelle f und die Annäherung aus c) mit Geogebra dar und berechne die durchschnittliche Abweichung von f und der Annäherungsfunktion.)

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Aufgabe 5 Integralfunktion

Paul, Sevda und Lucie wiederholen die Integralfunktion. Sie haben verstanden, dass jede Integralfunktion I_a einer Funktion f auch Stammfunktion derselben Funktion f ist. In der Lerngruppe herrscht nun jedoch Uneinigkeit darüber, ob umgekehrt jede Stammfunktion auch Integralfunktion ist.

Paul behauptet, dies sei für jede Funktion f der Fall.
Sevda meint dagegen, jede Funktion besäße auch Stammfunktionen, die keine Integralfunktionen sind.
Lucie zuletzt ist der Auffassung, dass es von der Funktion abhänge.

Begründe zunächst, weshalb jede Integralfunktion von f auch Stammfunktion von f ist. Überprüfe dann, wer Recht hat.

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Aufgabe 6 Integralfunktion

f bezeichnet im Folgenden eine im ganzen Definitionsbereich D knickfreie Funktion.

Streng steigende Monotonie ist für f wie folgt definiert:
Wenn für alle $a, b \in \textbf{D}$ mit a<b gilt: f(a)<f(b) , heißt f streng monoton steigend.

Aus dem Unterricht wissen wir, dass wir streng steigende Monotonie auch wie folgt untersuchen können:
Wenn für alle $x \in \textbf{D}$ gilt: f'(x)>0 , dann ist f streng monoton steigend.

Zeige mit Hilfe einer geeigneten Funktion f folgende Aussage:
Eine Funktion kann auch dann streng monoton steigend sein, wenn f'(x)>0 nicht für alle $x \in \textbf{D}$ gilt.

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Aufgabe 7 Lichtschalterproblem

Ein Hotel hat 100 Zimmer mit den Nummern 1 bis 100 und 100 Gäste. Jedes Zimmer hat einen Lichtschalter, der das Licht einschaltet, wenn es aus ist und es ausschaltet, wenn es an ist.

Zunächst sind alle Lichter ausgeschaltet.

Dann geht jeder Gast der Reihe nach durch jedes Zimmer:

Gast 1 drückt den Schalter jedes Zimmers.
Gast 2 drückt den Schalter jedes zweiten Zimmers, also von Zimmer 2, 4, 6, …
Gast 3 drückt den Schalter jedes dritten Zimmers, also von Zimmer 3, 6, 9, …
Gast 4…
…
Gast 100 drückt den Schalter jedes hundertsten Zimmers, also nur von Zimmer 100.

Beschreibe, wie für ein frei gewähltes Zimmer n (1 ≤ n ≤ 100) geprüft werden kann, ob nach dem Durchgang des letzten Gastes das Licht aus- oder eingeschaltet ist.

(Bonus: Simuliere das Lichtschalter-Problem mit einer Tabellenkalkulation oder mithilfe einer Programmiersprache und überprüfe, welche Lichter nach dem kompletten Durchlauf aus sind.)

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Aufgabe 8 Türme von Hanoi

Die „Türme von Hanoi“ sind ein altes asiatisches Rätselspiel, welches im 19. Jahrhundert im Westen eingeführt wurde.

Es besteht aus drei am Boden fixierten senkrechten Stäben, von denen zu Beginn die rechte und mittlere Stange unbelegt sind und die linke Stange eine n-stöckige Pyramide enthält, deren Stöcke aus gelochten Scheiben abnehmender Größe besteht. Die Abbildung rechts zeigt eine Holzversion des Spiels mit n=8 Stöcken.

Ziel des Spiels ist, die komplette Pyramide in möglichst wenigen Zügen auf den rechten Stab zu versetzen. Pro Zug darf genau eine Scheibe von einem Stab oben abgezogen und auf einen anderen Stab gesetzt werden. Dabei darf niemals eine Scheibe auf eine kleinere Scheibe abgelegt werden.

Untersuche in Abhängigkeit von n, in wie vielen Zügen N das Spiel optimalerweise gelöst werden kann.

_{Bild: anonym, Tower of Hanoi, CC BY-SA 3.0}

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Aufgabe 9 Die Rätsel um Johannes und Wilhelm

Der im Jahr 1919 geborene US-Mathematiker, Logiker, Zauberer und Philosoph Raymond M. Smullyan ist unter anderem für eine Reihe skurriler und lustiger Rätsel bekannt.

In einem aus mehreren Teilen bestehenden Rätsel Smullyians geht es um die beiden Protagonisten Johannes und Wilhelm. Jeder der beiden ist entweder ein Ritter, der selbstredend immer die Wahrheit sagt oder ein Knappe, der immer lügt.

Teil 1
Johannes sagt: „Wilhelm und ich sind beide Knappen.“
Wer von den beiden ist was?

Teil 2
Johannes sagt: „Wenn Wilhelm ein Knappe ist, so bin ich auch ein Knappe. Wenn Wilhelm ein Ritter ist, so bin ich auch ein Ritter.“
Wilhelm sagt: „Wenn Johannes ein Knappe ist, so bin ich ein Ritter. Wenn Johannes ein Ritter ist, so bin ich ein Knappe.“
Wer von den beiden ist was?

Teil 3
Dies ist der schwierigste Teil des Puzzles und wurde u. a. bekannt durch den Fantasy-Film „Labyrinth“.

Johannes und Wilhelm, von denen genau einer ein Ritter ist, stehen an einer gefährlichen Weggabelung, von dem zwei Pfade ausgehen: Der eine Pfad führt in die Freiheit und der andere zum sicheren Tod.
Johannes und Wilhelm wissen beide, welcher Pfad zur Freiheit führt.
Du als Rätsellöser darfst nun genau einem der beiden genau eine Ja-Nein-Frage stellen, um herauszufinden, welcher Pfad zur Freiheit führt. Welche Frage ist das?

Versuche, alleine oder in einer Gruppe die drei Teile des Rätsels zu lösen und begründe deine Lösungen.

AFB III	Kompetenzen k.A.	Bearbeitungszeit k.A.
Quelle Andreas Dinh		Lizenz CC BY-SA

Aufgabe 10 L’Hospital

Im Zusammenhang mit Exponentialfunktionen hast du von deinem Lehrer vielleicht erfahren, dass jede beliebige Exponentialfunktion f mit $f(x)=a\cdot q^x + b, x \in \mathbb{R}, a,b \in \mathbb{R}, q \in \mathbb{Q},$ „schneller wächst“ als jede beliebige Potenzfunktion g mit $g(x)= \tilde{a} \cdot x^r + \tilde{b}, x \in \mathbb{R}, \tilde{a},\tilde{b} \in \mathbb{R}, r \in \mathbb{Q}$ .
Gemeint ist mit dieser Formulierung: Ab einem bestimmten -Wert x_0 ist f(x)>g(x) für alle x>x_0 .

Betrachtet man z. B. die Funktionen $f(x) = \frac{1}{30} \cdot 1,01^x$ und $g(x)= x^{100}$ , so scheint dies nicht der Fall zu sein (vgl. Abbildung).

Aufgabe 10 Analysis.png

Untersuche, ob Exponentialfunktionen tatsächlich immer „schneller wachsen“ als Potenzfunktionen.

Verwende hierfür ein- oder mehrmalig die Regel von de L’Hospital, die für zwei ableitbare Funktionen f und g Folgendes besagt:

$\lim\limits_{x \rightarrow \infty}\frac{f(x)}{g(x)}= \lim\limits_{x \rightarrow \infty}\frac{f'(x)}{g'(x)}$

(Die Regel setzt man ein, wenn für $x \rightarrow \infty$ Zähler und Nenner beide gegen 0 oder beide gegen $-\infty$ oder, wie im Fall dieser Aufgabe, beide gegen $+\infty$ gehen.)