Aufgabe 1 Analysis 5_1 𝕋 𝕃
Die Abbildung zeigt den Graphen \(G_f\) der in \(\mathbb{R}\) definierten Funktion \(f: x \mapsto e^{-x}-e^{-2x}\).
\(G_f\) schneidet die x-Achse an der Stelle \(x_1=0\) und hat einen Hochpunkt an der Stelle \(x_H\).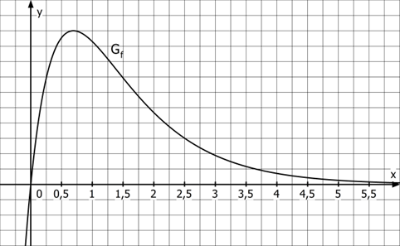
- Weise rechnerisch nach, dass \(x_1\) die einzige Nullstelle von \(f\) ist. [2 BE]
- Entscheide mit Hilfe der Abbildung, ob die folgenden Aussagen wahr oder falsch sind. Begründe jeweils deine Entscheidung. [3 BE]
- \(f^{\prime \prime} (0,5)>0\)
- \(\int_0^2 f(x)dx<2\cdot f(x_H )\)
| AFB k.A. | Kompetenzen k.A. | Bearbeitungszeit 15 min |
| Quelle Abitur 2024 | Lizenz k.A. | |
Aufgabe 2 Analysis 5_2 𝕋 𝕃
Gegeben ist die Funktion \(f\) mit \(f(x)=(x^2-4)\cdot(x-1)\) mit \(x\in \mathbb{R} \). Ihr Graph ist \(K_f\).
- Gib die Nullstellen von \(f \) an. [1 BE]
- Ermittle eine Gleichung der Tangente an \(K_f\) im Schnittpunkt von \(K_f\) mit der y-Achse.
Zeige, dass diese Tangente mit \(K_f \) einen gemeinsamen Punkt auf der x-Achse hat. [4 BE]
| AFB k.A. | Kompetenzen k.A. | Bearbeitungszeit 15 min |
| Quelle Abitur 2024 | Lizenz k.A. | |
Aufgabe 3 Lineare Algebra 5_3 𝕋 𝕃
Gegeben sind die beiden 2x2-Matrizen \(A\) und \(B\) sowie der Vektor \(\vec{v}\).
\[A=\left(\begin{matrix}2&-1\\-3&1\\\end{matrix}\right) \ \ \ \ \ \ \ \ \ \ B=\left(\begin{matrix}-1&-1\\-3&-2\\\end{matrix}\right)\ \ \ \ \ \ \ \ \ \ \vec{v}=\left(\begin{matrix}v_1\\v_2\\\end{matrix}\right) \]
- Zeige rechnerisch, dass \(B\) eine inverse Matrix zu \(A\) ist. [2BE]
- Gib eine mögliche Fragestellung an, die durch die Lösung des folgenden Gleichungssystems beantwortet werden kann. [3BE]
\[\begin{align}
2v_1-v_2&=1 \\
-3v_1+v_2&=2
\end{align}\]
| AFB k.A. | Kompetenzen k.A. | Bearbeitungszeit 15 min |
| Quelle Abitur 2024 | Lizenz k.A. | |
Aufgabe 4 Lineare Algebra 5_4 𝕋 𝕃
Für eine reelle Zahl \(a\) ist die Gerade \(g\) durch \(g: \vec{x}=\left(\begin{matrix}1\\2\\3 \end{matrix}\right)+t\cdot \left(\begin{matrix}1\\1\\a \end{matrix}\right)\) mit \(t\in\mathbb{R}\) gegeben.
Außerdem wird die Ebene \(E\) beschrieben durch \(E: x_1+x_2=3\)
- Bestimme den Wert von \(a\) so, dass sich \(g\) und \(E\) orthogonal schneiden. [2BE]
- Für \(a=1,5\) schneidet \(g\) die \(x_1\)-Achse im Punkt \(P\) und die Ebene \(E\) im Punkt \(S\left(1\left|2\right|3\right)\). Zudem ist der Punkt \(Q\left(1\left|2\right|0\right)\) bekannt.
Bestimme den Flächeninhalt des Dreiecks \(PQS\). [3BE]
| AFB k.A. | Kompetenzen k.A. | Bearbeitungszeit 15 min |
| Quelle Abitur 2024 | Lizenz k.A. | |