Zum Inhalt springen

BPE 1.2 Funktionen, Begriff, Definitions- und Wertebereich

Version 62.1 von Holger Engels am 2024/07/19 13:48
Inhalt

K1 Ich kann den Funktionsbegriff an Beispielen aus dem Alltag erläutern
K1 Ich kann entscheiden, ob eine gegebene Zuordnung eindeutig oder nicht eindeutig ist
K1 Ich kann die Begriffe Definitionsbereich, Definitionslücke und Wertebereich erläutern
K4 Ich kann den Definitions- und den Wertebereich einer grafisch, algebraisch oder verbal gegebenen Funktion ermitteln
K3 K4 Ich kann den Definitions- und den Wertebereich im Kontext einer Anwendungssituation ermitteln

Definition

Welche der beiden Zuordnungen ist eindeutig? Überlege jeweils, ob es sich um eine Relation oder um eine Funktion handelt!
Begründe deine Entscheidung!

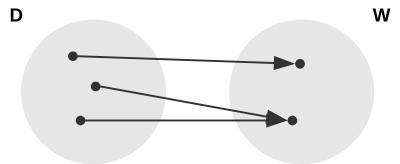
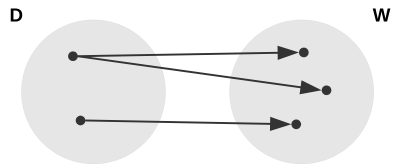
Venn Funktion.png Venn Relation.png

AFB   IKompetenzen   K5Bearbeitungszeit   k.A.
Quelle   KMapLizenz   CC BY-SA

In dieser Aufgabe soll die Entwicklung der Körpergröße eines weiblich Babys in Abhängigkeit vom Alter dargestellt werden.
Achsenkreuz.svg

  1. Skizziere ins Achsenkreuz eine mögliche Entwicklung.
  2. Nenne die von dir gewählte Wertebereich. Begründe deine Wahl.
  3. Nenne die von dir gewählte Definitionsbereich Begründe deine Wahl.
  4. Erläutere, ob dein Graph ein Funktionsgraph ist.
  5. Erläutere, ob die Umkehrung Alter in Abhängigkeit von der Körpergröße eine Funktion ist.
  6. Verändern sich Definitionsbereich und Wertebereich, wenn du die Aufgabe für ein männliches Baby löst? Begründe deine Antwort.
AFB   IIKompetenzen   K1 K3 K4Bearbeitungszeit   15 min
Quelle   Torben WürthLizenz   CC BY-SA

f(x) = \frac{1}{x}
f(x) = \sqrt{x}
Schaubild: Markiere den Wertebereich im Schaubild (Definitionsbereich ist markiert)
Schaubild: Verschobene Parabel
Geschwindigkeit - Bremsweg

AFB   IKompetenzen   K3 K4 K5Bearbeitungszeit   15 min
Quelle   Martin RathgebLizenz   CC BY-SA

f(x) = \frac{1}{x-2}
f(x) = \sqrt{x+1}
f(x) = \frac{x}{x}
Kaffee kühlt ab

AFB   IIKompetenzen   K3 K4 K5Bearbeitungszeit   15 min
Quelle   Martin RathgebLizenz   CC BY-SA

Stell dir vor, du möchtest die Zeit berechnen, die du benötigst, um zur Schule zu laufen.
Die Funktion T(x) gibt die benötigte Zeit in Minuten an, abhängig von der Geschwindigkeit x in km/min.
Die Funktion könnte wie folgt definiert sein: T(x)= \frac{d}{x}, wobei d die Entfernung zur Schule in Kilometern ist.
Nehmen wir an, du wohnst 5 km zur Schule entfernt.

  1. Erstelle die Funktion T(x), die die benötigte Zeit in Minuten in Abhängigkeit von der Geschwindigkeit x in km/h beschreibt.
  2. Bestimme die Definitionslücke der Funktion T(x).
  3. Erläutere, warum es in diesem Kontext sinnvoll ist, eine Definitionslücke zu haben.
  4. Zeichne den Graphen der Funktion T(x) und markiere die Definitionslücke.
AFB   IIKompetenzen   K1 K3 K4Bearbeitungszeit   15 min
Quelle   Ute Jutt, Ronja FrankeLizenz   CC BY-SA

Kompetenzmatrix und Seitenreflexion

K1K2K3K4K5K6
I001120
II203310
III000000
Bearbeitungszeit gesamt: 60 min
Abdeckung Bildungsplan
Abdeckung Kompetenzen
Abdeckung Anforderungsbereiche
Eignung gemäß Kriterien
Umfang gemäß Mengengerüst