BPE 1.4 Lineare Funktionen
K4 K5 Ich kann Geraden als Graphen linearer Funktionen deuten
K5 Ich kann die Gleichungen besonderer Geraden angeben
K1 K5 Ich kann begründen, dass eine Parallele zur y-Achse nicht Graph einer Funktion ist
K5 Ich kann den Steigungswinkel einer Geraden berechnen
K4 Ich kann den Steigungswinkel einer Geraden graphisch deuten
K5 Ich kann die Lagebeziehung zweier Geraden anhand ihrer Gleichungen und der Orthogonalitätsbedingung untersuchen
K5 K1 Ich kann lineare Ungleichungen geometrisch interpretieren
K5 Ich kann die Lösungsmengen linearer Ungleichungen mit Äquivalenzumformungen ermitteln
1 Besondere Geraden (4 min) 𝕀 𝕃
Das Schaubild zeigt vier Geraden. Alle können als Gleichung ausgedrückt werden. Drei stellen auch einen funktionalen Zusammenhang dar.
Gib jeweils eine Geradengleichung an.
Begründe, warum die vierte Gerade nicht Graph einer Funktion sein kann.
| AFB I - K1 K4 K5 | Quelle Holger Engels |
2 Taxifahrt (6 min) 𝕃
Für eine Taxifahrt fallen zunächst 5 Euro für die Anfahrt an. Dazu kommen pro angefangener gefahrener Minute 0,75 Euro.
Hinweis: Es werden Fahrten mit einer Dauer von bis zu 30 Minuten durchgeführt.
Stelle die oben beschriebene Situation grafisch dar.
Bestimme eine Gleichung, die den Sachverhalt mathematisch beschreibt.
| AFB I - K3 K4 K5 | Quelle Sabine Schäfer |
3 Funktionsvorschriften zuordnen (5 min) 𝕀 𝕃
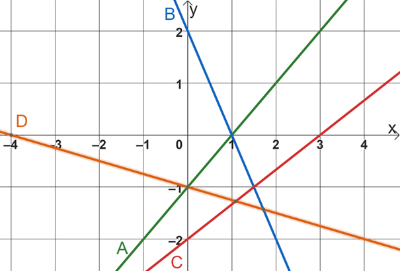Das Schaubild zeigt die Graphen von sechs verschiedenen linearen Funktionen. Gib an, welche Funktionsvorschrift zu welcher Geraden gehört. Begründe.
a) \(f\left(x\right)=x-1;x\in\mathbb{R} \)
b) \(f\left(x\right)=1 - x^2;x\in\mathbb{R}\)
c) \(f\left(x\right)=\frac23x-2;x\in\mathbb{R}\)
d) \(f\left(x\right)=-\frac14x-1;x\in\mathbb{R}\)
e) \(f\left(x\right)=-0,25 x-2;x\in\mathbb{R}\)
f) \(f\left(x\right)=2 - 2x;x\in\mathbb{R}\)
| AFB I - K4 K5 K6 | Quelle Sabine Schäfer |
4 Steigung (8 min) 𝕃
Die Baldwin Street im North East Valley ist mit einer maximalen Steigung von 1 : 2,86 die steilste Straße der Welt.
a) Stelle den Sachverhalt als Skizze dar.
b) Gib die Steigung der Straße in Prozent an.
c) Berechne den Steigungswinkel der Straße.
| AFB III - K3 K4 K5 | Quelle Holger Engels |
5 Abstand Graph Koordinatenursprung (8 min) 𝕋 𝕃
Die Abbildung zeigt den Graphen der in \(\mathbb{R}\) definierten linearen Funktion \( f\).
- Begründe, dass \(f(x)=\frac{1}{2}x+5\) gilt.
- Berechne den Abstand des Koordinatenursprungs zum Graphen.
| AFB III - K1 K2 K4 K5 | Quelle IQB e.V. | #iqb |
6 Steigungswinkel (5 min) 𝕃
Gegeben sind zwei lineare Funktionen f und g.
Bestimme jeweils den Steigungswinkel und die Steigung in Prozent.
a) \(f(x)=\frac{1}{2}x+1\)
b) 
| AFB I - K4 K5 | Quelle Holger Engels |
7 Orthogonale Funktion (5 min)
Bestimme den Funktionsterm einer linearen Funktion h, deren Graph orthogonal zu dem der Funktion g mit \(g(x)=3x-2\) ist und durch den Punkt P(-2|1) verläuft.
| AFB I - k.A. | Quelle Holger Engels |
8 Geradengleichung transformieren (5 min) 𝕃
Gegeben sei die Funktion \(f\left(x\right)=\frac{5}{4}x-4\).
Gebe jeweils die neue Funktionsgleichung an, wenn der Graph von \(K_{f}\)
- zuerst um 3 nach oben verschoben,
- anschließend an der x-Achse gespiegelt
- und abschließend an der y-Achse gespiegelt wird.
| AFB II - k.A. | Quelle Kim Fujan |
9 Ungleichung (5 min) 𝕃
Kim rechnet folgendes ..
\(-2x+1 > 0 \quad\,| -1\)
\(\Leftrightarrow -2x > -1 \quad| :(-2)\)
\(\Leftrightarrow x > 2\)
.. und stellt bei der Probe fest, dass irgendwas schief gelaufen sein muss. Erkläre!
| AFB I - k.A. | Quelle Holger Engels |
10 Tarife (5 min) 𝕃
Vergleiche die beiden Stromtarife:
\(f(x) = 20 + 0,3x\)
\(g(x) = 40 + 0,2x\)
Für welchen Verbrauch ist der Tarif mit dem höheren Grundbetrag günstiger?
Formuliere die Fragestellung als Ungleichung. Löse mittels Äquivalenzumformungen und graphisch.
| AFB I - k.A. | Quelle Holger Engels |