BPE 2 Einheitsübergreifend

Version 87.1 von Martin Rathgeb am 2024/12/23 00:49

Inhalt

AFB I Weg zur Schule
AFB II Potenzgleichungen lösen - graphisch und rechnerisch Lineare Regression Korrelation
AFB III Füllstände Spiegeln an der Winkelhalbierenden Spiegeln an der Winkelhalbierenden (alt)

Aufgabe 1 Weg zur Schule 𝕋 𝕃

Kay möchte die Laufzeit für den Weg vom Bahnhof zur Schule berechnen. Die Laufzeit wird modelliert durch die Funktion mit $t(v)= \frac{d}{v}$ (Geschwindigkeit in km/min; Entfernung in km; Laufzeit t(v) in min). Eine Messung hat ergeben, dass die Schule vom Bahnhof 5 km entfernt liegt.

Erstelle die Funktion , die die benötigte Zeit in Minuten in Abhängigkeit von der Geschwindigkeit in km/h beschreibt.
Bestimme die Definitionslücke der Funktion .
Erläutere, warum es in diesem Kontext sinnvoll ist, eine Definitionslücke zu haben.
Zeichne den Graphen der Funktion und markiere die Definitionslücke.

AFB I	Kompetenzen K1 K3 K4	Bearbeitungszeit 20 min
Quelle Ute Jutt, Ronja Franke		Lizenz CC BY-SA

Aufgabe 2 Potenzgleichungen lösen - graphisch und rechnerisch 𝕃

Gegeben sind die Funktionen f und g mit den Funktionsgleichungen $f(x)=\sqrt{-x+1}$ und $g(x)=-\sqrt{x+5}+3$ .

Gib jeweils die maximale Defintionsmenge und den zugehörigen Wertebereich an.
Zeichne die Funktionsgraphen zu den Funktionen in ein gemeinsammes Koordinatensystem im Intervall .
Bestimme die Lösungen der Wurzelgleichung $\sqrt{-x+1} = -\sqrt{x+5}+3$ graphisch.
Berechne die Lösungen und vergleiche deine berechneten Lösungen mit den graphischen Lösungen aus c).

AFB II	Kompetenzen K4 K5	Bearbeitungszeit 15 min
Quelle Martin Stern, Niklas Wunder		Lizenz CC BY-SA

Aufgabe 3 Lineare Regression 𝕃

Nachfolgend ist die Menge freier Chlorreste in ppm (parts per million) in Schwimmbecken als Funktion der Zeit (in Stunden)
nach der Behandlung mit Chemikalien angegeben

Zeit	2	4	6	8	10	12
Menge	1,7	1,5	1,2	1,0	1,0	0,8

Bestimme mit Hilfe des Taschenrechners eine Ausgleichsgerade für die gegebenen Messwerte. Notiere auch den Korrelationskoeffizienten r.
Berechne mit Hilfe deiner Ausgleichsgeraden einen Näherungswert zum Zeitpunkt 7 Stunden nach dem Messbeginn.

AFB II	Kompetenzen K3 K4 K5	Bearbeitungszeit 10 min
Quelle Universität Köln Dr.C.Lange		Lizenz CC BY-SA

Aufgabe 4 Korrelation 𝕃

Die Tabelle gibt Daten aus seriösen Quellen über die Anzahl der Storchenpaare und die Einwohneranzahl in den Jahren 1930 bis 1936 in Oldenburg wieder.

Jahr	1930	1931	1932	1933	1934	1935	1936
Anzahl der Storchenpaare	132	142	166	188	240	250	252
Anzahl der Einwohner	55400	55400	65000	67700	69800	72300	76000

a) Bestimme die Ausgleichsgerade zwischen Storchenpaaren und Einwohnerzahlen sowie den Korrelationskoeffizienten.
b) Alex behauptet, dass die Störche hauptsächlich für den Einwohnerzuwachs in Oldenburg verantwortlich waren. Nimm dazu begründet Stellung und beziehe den in a) berechneten Korrelationskoeffizienten in deine Begründung mit ein.

AFB II	Kompetenzen K1 K3 K5	Bearbeitungszeit 15 min
Quelle Niklas Wunder		Lizenz CC BY-SA

Aufgabe 5 Füllstände 𝕃

Die beiden abgebildeten Gefäße werden mit Wasser gefüllt. Ist es möglich, dass bei gleichem Füllstand genau gleich viel Wasser in den Gefäßen ist?
Füllstände Gefäße.PNG

Finde gegebenenfalls diesen Füllstand und das zugehörige Wasservolumen heraus.

#problemlösen

AFB III	Kompetenzen K2 K5 K6	Bearbeitungszeit 25 min
Quelle Problemlösegruppe		Lizenz CC BY-SA

Aufgabe 6 Spiegeln an der Winkelhalbierenden 𝕃

Graphische Transformationen gehören zu den Grundwerkzeugen der Mathematik. Neben Verschiebungen, Streckungen und Spiegelungen an den Achsen gibt es eine besondere Transformation, die in ihrer Bedeutung oft übersehen wird: die Spiegelung an der ersten Winkelhalbierenden, d.h., an der Geraden mit Gleichung y=x . Diese Transformation ist weit mehr als eine Spielerei, denn sie führt direkt zur Bestimmung der Umkehrfunktion einer gegebenen Funktion.

Betrachten wir dafür zunächst ein Beispiel. Für alle Funktionen schränkt man den Definitionsbereich auf x> 0 ein. Wieso dies sinnvoll ist wird später klar. Um die Funktionsgleichung nach Spiegelung rechnerisch zu ermitteln nimmt man die Funktionsgleichung, z.B. y=x^2 , löst diese nach x auf und vertauscht anschließend die Variablen so erhält man den gespiegelten Funktionsgraphen mit passender Funktionsgleichung.

$\begin{align*} y=x^2 \;\; | \,\sqrt{\phantomtext}\\ x=\sqrt{y}\;\;$
Vertausche x und y miteinander um die Funktionsgleichung des gespiegelten Funktionsgraphens zu erhalten.
$y=\sqrt{x} \end{align*}$

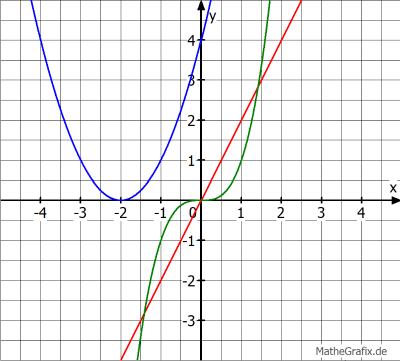
Bestimme nun die an der ersten Winkelhalbierenden gespiegelten Funktionen für folgende Beispiele:

Zeichne außerdem die gespiegelten Graphen und überprüfe, wie sich diese zur Winkelhalbierenden verhalten.
Die in a) berechneten Funktionen nennt man Umkehrfunktionen ( $f^{-1}$ ). Untersuche den Ausdruck $f^{-1}(y)$ für und beschreibe, was dir auffällt.
Abschließend stellt sich die Frage: Warum muss der Definitionsbereich der Funktion f verkleinert werden, wenn die Umkehrfunktion berechnet wird? Begründe diese Einschränkung mit den Ergebnissen aus a) und b).

AFB III	Kompetenzen K4	Bearbeitungszeit 12 min
Quelle Niklas Wunder, Martin Rathgeb		Lizenz CC BY-SA

Aufgabe 7 Spiegeln an der Winkelhalbierenden (alt)

Neben der Spiegelung an der x- und y- Achse kann man auch an der ersten Winkelhalbierenden (gegeben durch y=x) einen Funktionsgraphen spiegeln. Für alle Funktionen schränkt man den Definitionsbereich auf x> 0 ein. Wieso dies sinnvoll ist wird später klar. Um die Funktionsgleichung nach Spiegelung rechnerisch zu ermitteln nimmt man die Funktionsgleichung, z.B. y=x^2 , löst diese nach x auf und vertauscht anschließend die Variablen so erhält man den gespiegelten Funktionsgraphen mit passender Funktionsgleichung.

$\begin{align*} y=x^2 \;\; | \,\sqrt{\phantomtext}\\ x=\sqrt{y}\;\;$
Vertausche x und y miteinander um die Funktionsgleichung des gespiegelten Funktionsgraphens zu erhalten.
$y=\sqrt{x} \end{align*}$

Bestimme die an der ersten Winkelhabierenden gespiegelten Funktionen $f(x)=\frac{1}{x}; g(x)= \frac{1}{x^2}$ und $h(x)= \frac{2\,x+3}{-4\,x-2}$ . Hinweis:
Bestimme graphisch den an der ersten Winkelhalbierenden gespiegelten Graphen zu den drei dargestellten Graphen.
Die in a) berechneten Funktionen nennt man auch Umkehrfunktionen (Abkürzung $f^{-1}$ ) . Berechne den Funktionsterm $f^{-1}(f(x))$ . Beschreibe deine Beobachtung. Hinweis: Setze dazu den Term der Funktionsgleichung in die in a) berechnete Umkehrfunktion $f^{-1}$ ein und fasse zusammen.
Begründe mit Hilfe deiner Lösungen von a) und b) wieso der Definitionsbereich der Funktion verkleinert werden muss, wenn man die Funktionsgleichung der Umkehrfunktion berechnet.