BPE 3.1 Eigenschaften und Formen
K5 Ich kenne die allgemeine Form der Polynomfunktion
K4 Ich kenne die Produktform der Polynomfunktion
K3 K4 Ich kann die für den Anwendungsfall geeignete Darstellungsform wählen
K1 K4 Ich kann die Wahl der Darstellungsform im Anwendungskontext begründen
1 Schaubilder zuordnen Teil 1 (5 min) 𝕀 𝕃
 Ordne die Funktionsterme den 5 Schaubildern zu. Begründe deine Wahl.
Ordne die Funktionsterme den 5 Schaubildern zu. Begründe deine Wahl.
- \(f_1(x)=x^3\)
- \(f_2(x)=-x^2\cdot(x-3)\)
- \(f_3(x)=0{,}5\,x^3\)
- \(f_4(x)=0{,}5\,x^3+2\,x^2-3\)
- \(f_5(x)=-x^3-2\,x^2+2\)
| AFB II - K4 | Quelle Niklas Wunder, Katharina Schneider |
2 Schaubilder zuordnen Teil 2 (5 min) 𝕃
 Ordne die Funktionsterme den 5 Schaubildern zu. Begründe deine Wahl.
Ordne die Funktionsterme den 5 Schaubildern zu. Begründe deine Wahl.
- \(f_1(x)=-0{,}25\,x^4\)
- \(f_2(x)=-0{,}5\,x^4-1{,}5\,x^3-1{,}5\,x^2-1\)
- \(f_3(x)=-x^4\)
- \(f_4(x)=-x^4-x^3+2x^2+2\)
- \(f_5(x)=-0{,}3\cdot (x+2)^2\cdot(x-2)^2+4\)
| AFB II - K4 | Quelle Niklas Wunder, Katharina Schneider |
3 Produktform (10 min) 𝕃
Bestimme zu den abbgebildeten Funktionsgraphen eine mögliche Funktionsgleichung in Produktform.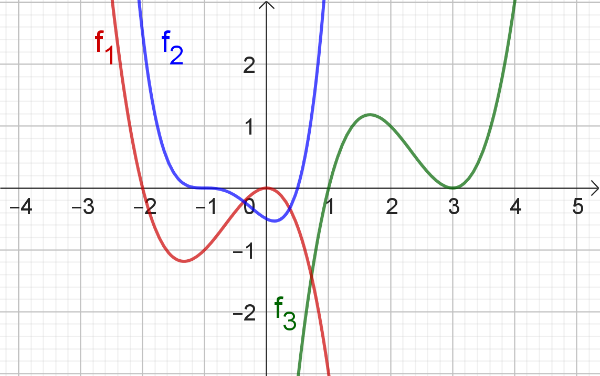
| AFB I - K4 | Quelle Juliane Maier |
4 Skizzieren (k.A.)
Gegeben ist die Funktion \(f\) mit \(D=\mathbb{R}\). Skizziere den Funktionsgraphen.
- \(f(x)=(x-2)^3\)
- \(f(x)=x^4-x^2\)
| AFB I - K4 | Quelle Juliane Maier |
5 Immer, manchmal, nie (12 min) 𝕃
Beurteile, ob die folgenden Aussagen immer, nie oder manchmal unter bestimmten Bedingungen zutreffen. Begründe deine Entscheidung.
- Der Graph von \(f\) mit \(f(x)=-3\cdot x^n \) verläuft für ein gerades n von links unten nach rechts unten.
- Der Graph einer Polynomfunktion mit einem ungeraden Grad hat mindestens eine Nullstelle.
- Der Graph einer zum Ursprung symmetrischen Funktion geht durch den Punkt (1|1).
- Es gibt mindestens eine Funktion 5.Grades, die keine Nullstelle besitzt.
- Der Graph einer achsensymmetrischen Funktion hat mindestens eine Nullstelle.
- Durch die beiden Punkte P(-2|1) und Q(2|2) verläuft kein Graph einer Funktion vierten Grades.
| AFB III - K1 K5 | Quelle Niklas Wunder, Katharina Schneider |
6 Darstellungsformen umwandeln (15 min) 𝕃
Wandle in die entsprechend andere Darstellungsform um (Hauptform bzw. Produktform).
- \(f(x)=-\frac{1}{16}\cdot (x-2)^2\cdot (x-8)\)
- \(f(x)=(x-3)\cdot (x^2+3x+9)\)
- \(f(x)=3\,x^3-33\,x^2+96\,x-84\)
Hinweis: Die Funktion f besitzt nur die beiden Nullstellen \( x_1 =1 \) und \( x_2 =7 \). - \(f(x)=-2\,x^4+18\,x^2+8\,x-24\)
Hinweis: Die Funktion f besitzt nur die Nullstellen \( x_1 =-2, x_2=1 \) und \( x_3 =3 \).
| AFB II - K5 | Quelle Niklas Wunder, Katharina Schneider |
7 Parabelmaschine (20 min) 𝕃
Denke dir zwei Zahlen, eine positiv, eine negativ.
Wenn du diese Zahlen quadrierst, erhältst du zwei Punkte auf der Normalparabel.
Ermitteln Sie, wo die Verbindungslinie dieser zwei Punkte die y-Achse schneidet!
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II - K2 K5 | Quelle Simon Oswald | #problemlösen |
8 Parameter bestimmen (k.A.) 𝕃
Gegeben sind die Funktionsterme der Funktionen \(f,g,h,k\) sowie Punkte, durch die das Schaubild der jeweiligen Funktion verläuft. Bestimme die fehlenden Parameter für jede Funktion.
- \(f(x)=a\cdot (x-3)\cdot (x-5)^2\) mit \( P(5|20) \)
- \(g(x)=a\cdot (x-b)^2\cdot (x-7)^2\) mit \( P(2|0) \) und \(Q(-2|-8)\)
- \(h(x)= a\,x^4-3x^2+c\) mit \( P(0|5) \) und \( Q(4|-11) \)
- \( k(x)= a\cdot(x-b)^3-7 \) mit \( P(2|-7) \) und \( Q(0|-5) \)
| AFB III - K4 K5 | Quelle Katharina Schneider,Niklas Wunder |
Inhalt für Lehrende (Anmeldung erforderlich)
