Zum Inhalt springen

BPE 4.5 Logarithmus und Exponentialgleichungen

Version 121.2 von Elke Hallmann am 2025/02/26 14:40
Inhalt

K5 Ich kann Logarithmus nutzen, um eine Exponentialgleichung zu lösen
K5 Ich kann eine geeignete Strategie wählen, um eine gegebene Exponentialgleichung zu lösen
K1 Ich kann die Wahl einer Lösungsstrategie für eine Exponentialgleichung begründen
K5 Ich kann Exponentialgleichungen algebraisch lösen
K4 K6 Ich kann die Lösungen einer Exponentialgleichung als Nullstelle interpretieren
K4 K6 Ich kann die Lösungen einer Exponentialgleichung als Schnittstelle zweier Funktionen interpretieren

Aufgaben:
– Logarithmus: graphisches Ermitteln vs. Operator
Lösen von Exponentialgleichungen:
– Vokabelheft für Umkehroperationen
– Umkehrung der Rechenoperationen (Logarithmieren!) zzgl. Grundrechenarten
– Faktorisierung durch Ausklammern und Satz vom Nullprodukt zzgl. Grundrechenarten
– Substitution (abc-Formel, pq-Formel, Typ I) zzgl. Grundrechenarten
- Näherungslösungen

Gleichungen:
x+y = e > y = e - x
x*y = e > y = e / x
e^y = x > y = lncancel

Nenne jeweils eine passende Gleichung:
 
Die Gleichung kann ich nach x auflösen, indem ich\( \ldots \)

  1. \( \ldots \) die Terme auf beiden Seiten durch 5 dividiere und damit die Lösung \( x = \frac{2}{5} \) erhalte.
  2. \( \ldots \) von beiden Termen die 5-te Wurzel ziehe und damit die Lösung \( x = \sqrt[5]{2} \) erhalte.
  3. \( \ldots \) die Terme auf beiden Seiten zur Basis 5 logarithmiere und damit die Lösung \( x = \log_5(2) \) erhalte.
AFB   IIKompetenzen   K5Bearbeitungszeit   5 min
Quelle   Elke Hallmann, Martin Rathgeb, Dirk Tebbe, Martina WagnerLizenz   CC BY-SA

Nenne möglichst viele (wahre) Gleichungen der folgenden Formen, wobei \( a, b, c \in \{2; 3; 4; \ldots; 16\} \) gelten soll:
\( c = a^b\:; \qquad c = \sqrt[a]{b}\:; \qquad c = \log_a(b)\:; \qquad c = a\cdot b\:. \)

AFB   IKompetenzen   K2 K5Bearbeitungszeit   10 min
Quelle   Martin Rathgeb, Dirk TebbeLizenz   CC BY-SA

Ordne zu:

Implizite GleichungenExplizite GleichungenWertetabellenSchaubilder
\( x^{-3} = 8 \)\( x = \sqrt[3]{8} \)
x0123
y1248
2^xund8.svg
\( 2^x = 8 \)\( x = -\log_{2}(8) \) 
x0123
y01827
2^-xund8.svg
\( 2^{-x} = 8 \)\( x = \log_{2}(8) \) 
x0123
y1\frac{1}{2}827
x^3und8.svg
\( 2^x = 8 \)\( x = x = \frac{1}{\sqrt[3]{8}} \) 
x0123
y01827
x^-3und8.svg
AFB   IKompetenzen   K5Bearbeitungszeit   5 min
Quelle   Elke Hallmann, Martin Rathgeb, Dirk TebbeLizenz   CC BY-SA

Ordne (ohne WTR!) die Terme ihren Werten gemäß den Kästchen über dem Zahlenstrahl zu. Trage dafür die jeweiligen Buchstaben in die Kästchen ein.

Logarithmus_neu.svg

  1. \( \log_{10}(0.1) \)
  2. \( \log_{100}(0.1) \)
  3. \( \log_{0.1}(0.1) \)
  4. \( \log_{10}(1000) \)
  5. \( \log_{10}(50) \)
  6. \( \log_{0.1}(1000) \)
  7. \( \log_{10}(1) \)
  8. \( \log_{100}(10) \)
  9. \( \log_{10}(10) \)
AFB   IIKompetenzen   K4 K5Bearbeitungszeit   10 min
Quelle   Elke Hallmann, Martin Rathgeb, Dirk TebbeLizenz   CC BY-SA

Ermittle die Lösung der Gleichung \( 2^x = 5 \) graphisch und rechnerisch.

AFB   IKompetenzen   K5Bearbeitungszeit   5 min
Quelle   Elke Hallmann, Martin Rathgeb, Dirk TebbeLizenz   CC BY-SA

Aufgabe als Dokument im Anhang ‚unten‘.

AFB   IKompetenzen   K5Bearbeitungszeit   6 min
Quelle   Martin RathgebLizenz   CC BY-SA

Bestimme die Lösung der folgenden Gleichungen:

Typ 1 UmkehroperationenTyp 2 AusklammernTyp 3 Substitution
\(x^2 = 2\)\(x^2-2x = 0\)\(x^4-40x^2+144 = 0\)
\(x^4 = e\)\(2x^e = x^{2e}\)\(x^{2x}+x^e+1 = 0\)
\(e^x = e\)\(2e^x = e^{2x}\)\(10^{6x}-2\cdot 10^{3x}+1 = 0\)
\(3e^x = \frac{1}{2}e^{-x}\)\(x\cdot 3^x+4\cdot 3^x = 0\)\(3e^x-1 = \frac{1}{3}e^{-x}\)
AFB   IIKompetenzen   K5Bearbeitungszeit   20 min
Quelle   Elke Hallmann, Martin Rathgeb, Dirk Tebbe, Martina WagnerLizenz   CC BY-SA

Nenne eine passende Gleichung. Die Gleichung kann ich nach x auflösen, indem ich \( \ldots \)

  1. \( \ldots \) die Terme auf beiden Seiten durch 5 dividiere und damit die Lösung \( x = \frac{2}{5} \) erhalte.
  2. \( \ldots \) von beiden Termen die 5-te Wurzel ziehe und damit die Lösung \( x = \sqrt[5]{2} \) erhalte.
  3. \( \ldots \) die Terme auf beiden Seiten zur Basis 5 logarithmiere und damit die Lösung \( x = \log_5(2) \) erhalte.
    {{/aufgabe}}

Bestimme die Lösungsmenge der Exponentialgleichung:

  1. \( 4\cdot 0,5^x=100 \)
  2. \( e^x=3 \)
  3. \( 2e^x-4=8 \)
  4. \( 2e^{-0.5x}=6\)
  5. \( e^x=-5 \)
AFB   IKompetenzen   K5Bearbeitungszeit   15 min
Quelle   Elke Hallmann, Martin Rathgeb, Dirk TebbeLizenz   CC BY-SA

Bestimme die Lösungsmenge der Gleichung:

  1. \( 2x=x^{2} \)
  2. \( 2x^e=x^{2e} \)
  3. \( 2e^x=e^{2x} \)
AFB   IIKompetenzen   K5Bearbeitungszeit   12 min
Quelle   Martin RathgebLizenz   CC BY-SA

Bestimme die Lösungsmenge der Gleichung:

  1. \( 2x-3=x^{2} \)
  2. \( 2x^e-3=x^{2e} \)
  3. \( 2e^x-3=e^{2x} \)
  4. \( 2e^{x-3}=e^{2x-3} \)
AFB   IIIKompetenzen   K5Bearbeitungszeit   12 min
Quelle   Martin RathgebLizenz   CC BY-SA

Bestimme die Lösungsmenge der folgenden Exponentialgleichungen

  1. \( 3^{x+1}=81 \)
  2. \( 5^{2x}=25^{2x+2} \)
  3. \( 10^{x}=500\)
  4. \( 2^{x+3}=4^{x-1} \)
AFB   IKompetenzen   K5Bearbeitungszeit   5 min
Quelle   Niklas WunderLizenz   CC BY-SA

Löse mit Hilfe der nebenstehenden Abbildung folgende Exponentialgleichungen näherungsweise. Hinweis: Ordne die linke und die rechte Seite der jeweiligen Gleichung passend den Funktionsgraphen zu.

  1. \( 2^x=(\frac{3}{4})^x+2 \)
  2. \( 7-e^{x-3}=(\frac{3}{4})^x+2 \)
  3. \( 2^x=1{,}5^{x+2}-0{,}5 \)
  4. \( 7-e^{x-3}=4-\frac{1}{2}\,x \)

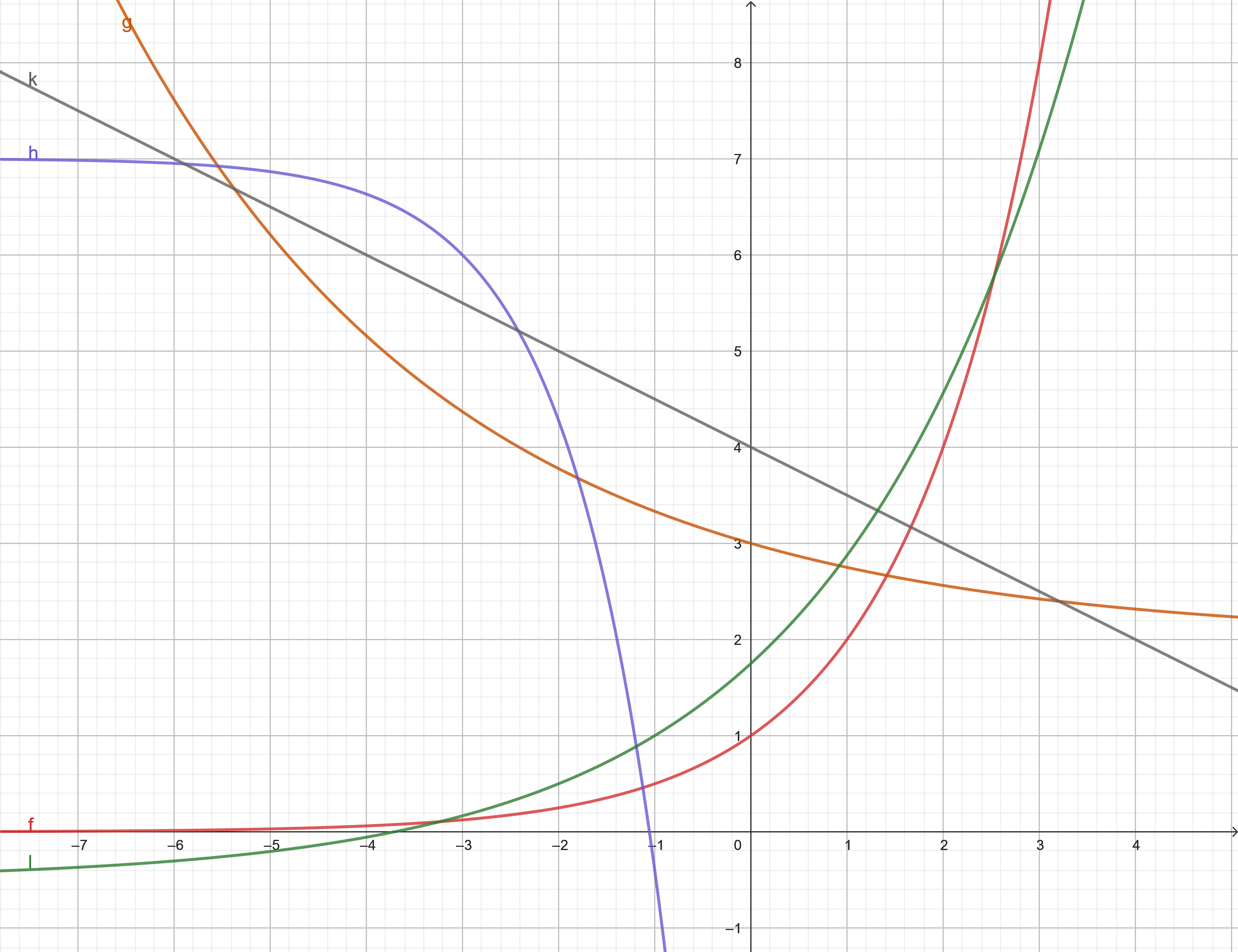
ExpGlei.svg

AFB   IIKompetenzen   K4 K6Bearbeitungszeit   5 min
Quelle   Niklas WunderLizenz   CC BY-SA

Kompetenzmatrix und Seitenreflexion

K1K2K3K4K5K6
I010060
II000241
III000010
Bearbeitungszeit gesamt: 110 min
Abdeckung Bildungsplan
Abdeckung Kompetenzen
Abdeckung Anforderungsbereiche
Eignung gemäß Kriterien
Umfang gemäß Mengengerüst