- \[\overrightarrow{f_1}= 3 \vec{b}+\frac{5}{3} \vec{c} = \textcolor{green!50!black}{\left(\begin{array}{c} -30 \\ 80 \end{array}\right)}\]\[\overrightarrow{f_2}= \vec{a}-2 \vec{b}+\frac{7}{2} \vec{c} = \textcolor{green!50!black}{\left(\begin{array}{c} 45 \\ 95 \end{array}\right)}\]\[\overrightarrow{f_3}= \vec{a}- \vec{b}+\frac{3}{4} \vec{d} = \textcolor{green!50!black}{\left(\begin{array}{c} 95 \\ 0 \end{array}\right)}\]\[\overrightarrow{f_4}= 2\vec{b}-6,5\vec{c} = \textcolor{green!50!black}{\left(\begin{array}{c} -20 \\ -175 \end{array}\right)}\]
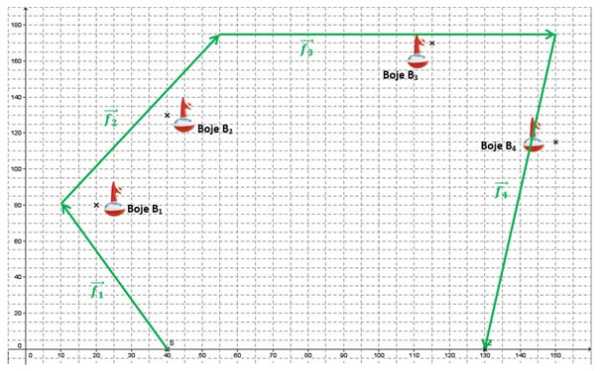
Die letzte Boje wird nicht von außen umsegelt, das Team wählt also einen kürzeren Weg als erlaubt. Der Kurs ist somit nicht regelkonform. - \[|\overrightarrow{s_1}|=\sqrt{(-20)^2+80^2}=20\sqrt{17}\approx 82,46\]\[|\overrightarrow{s_2}|=\sqrt{20^2+50^2}=10\sqrt{29}\approx 53,85\]\[|\overrightarrow{s_3}|=\sqrt{75^2+40^2}=85\]\[|\overrightarrow{s_4}|=\sqrt{35^2+(-55)^2}=5\sqrt{170}\approx 65,19\]\[|\overrightarrow{s_5}|=\sqrt{(-20)^2+(-115)^2}=5\sqrt{545} \approx 116,73\]\[|\overrightarrow{s_1}|+|\overrightarrow{s_2}|+|\overrightarrow{s_3}|+|\overrightarrow{s_4}|+|\overrightarrow{s_5}|\approx 403,23\]
Sie legen 403,23 km zurück.
Sei \(v_{Straight}\) die Geschwindigkeit des Segelteams Straight.
Das Segelteam Straight legt bis zur Boje 2 die Strecke \(|\overrightarrow{s_1}|+|\overrightarrow{s_2}|=20\sqrt{17}+10\sqrt{29}\approx 136,31\) zurück. Die Dafür benötigte Zeit berechnet sich durch
\(t_{Straight}=\frac{s_{Straight}{v_{Straight}}\approx \frac{136,31}{v_{Straight}}\).Die Strecke, die der Photograph zurücklegt berechnet sich durch \(|\overrightarrow{SB_2}|=\sqrt{(40-40)^2+(130-0)^2}=\sqrt{130^2}=130\). Die dafür benötigte Zeit ist
\(t_{Photograph}=\frac{s_{Photograpph}{v_{Photograph}}=\frac{s_{Photograpph}{\frac{2}{3}v_{Straight}}=\frac{\frac{3}{2}\cdot 130}{v_{Straight}}=\frac{195}{v_{Straight}}\)Da \(195>136,31\) ist \(t_{Photograph}>t_{Straight}\).
Somit erreicht der Photograph die Position \(B_2(40|130)\) nicht vor dem Team Straight.
