Problemlösen AFB III
Eingangklasse
Jahrgangsstufen
BPE 8 Übergreifende Problemlöseaufgaben
Aufgabe 2 Kreismittelpunkt 𝕃
Gegeben ist ein Kreis. Auf diesem werden zufällig drei Punkte A, B und C ausgewählt und durch ein Dreieck miteinander verbunden.
Mit welcher Wahrscheinlichkeit liegt der Mittelpunkt des Kreises innerhalb des Dreiecks (oder auf einer Dreiecksseite)?
| AFB III | Kompetenzen K2 K4 K5 K6 | Bearbeitungszeit 20 min |
| Quelle Stefan Rosner | Lizenz CC BY-SA | |
BPE 12.4 Stammfunktionen, Graphisches Aufleiten
Aufgabe 18 Aufleiten ln (eAN) 𝕃
Im Unterricht eines J2-Kurses soll die Funktion \(f(x)=\frac{1}{2x}\) aufgeleitet werden. Johann rechnet mit der Kettenregel der Aufleitung wie folgt: \(F(x)=\frac{1}{2}\ln(|2x|)\). Johannes mag die Kettenregel nicht und formt den Term von f zunächst um: \(f(x)=\frac{1}{2}\cdot\frac{1}{x}\), denn danach wird die Aufleitung ganz einfach: \(F(x)=\frac{1}{2}\ln(|x|)\). Die beiden geraten in eine Diskussion darüber, welche Lösung richtig ist. Überprüfe dies.
| AFB III | Kompetenzen K5 | Bearbeitungszeit 15 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
Aufgabe 19 Funktion gesucht 𝕃
Bestimme einen Funktionsterm, dessen Graph an der Stelle x = 2 die Tangente \(g(x)=\frac12 x+1\) hat.
| AFB III | Kompetenzen K2 K5 | Bearbeitungszeit 11 min |
| Quelle Holger Engels | Lizenz k.A. | |
Aufgabe 23 L’Hospital (M+) 𝕃
Im Zusammenhang mit Exponentialfunktionen hast du von deinem Lehrer vielleicht erfahren, dass jede beliebige Exponentialfunktion f mit \( f(x)=a\cdot q^x + b, x \in \mathbb{R}, a,b \in \mathbb{R}, q \in \mathbb{Q}, \) „schneller wächst“ als jede beliebige Potenzfunktion g mit \( g(x)= \tilde{a} \cdot x^r + \tilde{b}, x \in \mathbb{R}, \tilde{a},\tilde{b} \in \mathbb{R}, r \in \mathbb{Q} \).
Gemeint ist mit dieser Formulierung: Ab einem bestimmten \(x\)-Wert \(x_0 \) ist \( f(x)>g(x) \) für alle \(x>x_0 \).
Betrachtet man z. B. die Funktionen \( f(x) = \frac{1}{30} \cdot 1,01^x\) und \( g(x)= x^{100} \), so scheint dies nicht der Fall zu sein (vgl. Abbildung).
Untersuche, ob Exponentialfunktionen tatsächlich immer „schneller wachsen“ als Potenzfunktionen.
Verwende hierfür ein- oder mehrmalig die Regel von de L’Hospital, die für zwei ableitbare Funktionen f und g Folgendes besagt:
(Die Regel setzt man ein, wenn für \( x \rightarrow \infty\) Zähler und Nenner beide gegen 0 oder beide gegen \(-\infty\) oder, wie im Fall dieser Aufgabe, beide gegen \(+\infty \) gehen.)
Für die Aufgabe nicht benötigte Zusatzbemerkung: Die Regel gilt auch für \( x \rightarrow -\infty\) und für \( x \rightarrow x_0, x_0 \in \mathbb{R}\).
| AFB III | Kompetenzen K2 K4 K5 K6 | Bearbeitungszeit 30 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
BPE 13.2 Hauptsatz der Differenzial- und Integralrechnung, Bestimmtes Integral
Aufgabe 25 Integralfunktion 𝕃
Paul, Sevda und Lucie wiederholen die Integralfunktion. Sie haben verstanden, dass jede Integralfunktion \(I_a\) einer Funktion f auch Stammfunktion derselben Funktion f ist. In der Lerngruppe herrscht nun jedoch Uneinigkeit darüber, ob umgekehrt jede Stammfunktion auch Integralfunktion ist.
- Paul behauptet, dies sei für jede Funktion f der Fall.
- Sevda meint dagegen, jede Funktion besäße auch Stammfunktionen, die keine Integralfunktionen sind.
- Lucie zuletzt ist der Auffassung, dass es von der Funktion abhänge.
Begründe zunächst, weshalb jede Integralfunktion von f auch Stammfunktion von f ist. Überprüfe dann, wer Recht hat.
| AFB III | Kompetenzen K2 K1 K5 | Bearbeitungszeit 30 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
Aufgabe 27 Uneigentliches Integral (M+) 𝕃
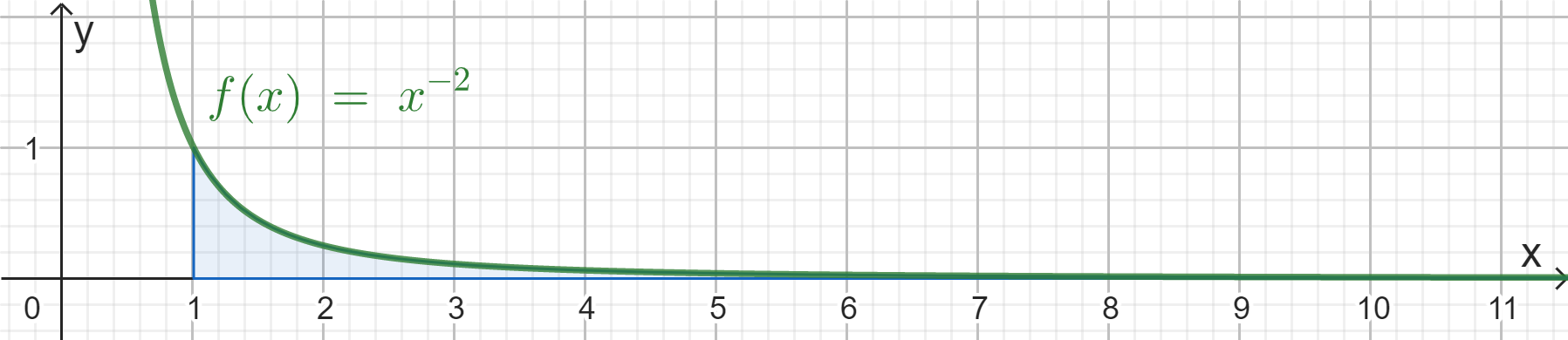
Betrachtet wird für negative rationale Zahlen q die Potenzfunktion p mit \(p(x)=x^q;\: x\neq 0\).
Für \(b \rightarrow \infty\) heißt \(U_q=\int_1^b{p(x)}\cdot dx\) uneigentliches Integral über p, falls \(U_q\) eine reelle Zahl ergibt.
Überprüfe, für welche Werte von q das uneigentliche Integral \(U_q\) existiert.
| AFB III | Kompetenzen K2 K5 | Bearbeitungszeit 40 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
Aufgabe 27 Annäherung 𝕃
 In \([0; \pi/2]\) soll die Funktion f mit \(f(x)=\cos{x}\) durch eine Potenzfunktion g mit \(g(x)=1-ax^q\) angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.
In \([0; \pi/2]\) soll die Funktion f mit \(f(x)=\cos{x}\) durch eine Potenzfunktion g mit \(g(x)=1-ax^q\) angenähert werden, wobei q eine positive rationale Zahl ist und a so gewählt wird, dass der Graph von g ebenfalls bei π/2 eine Nullstelle besitzt.
- Bestimme a in Abhängigkeit von q.
Begründe, weshalb ein kleiner Wert des Integrals
\[\int_0^{\frac{\pi}{2}} f(x)-g(x)\cdot dx\]ein guter Hinweis dafür ist, dass g eine gute Näherung für f ist.
- Finde eine Potenzfunktion g, die f gemäß des Kriteriums von b) gut annähert.
(Bonus: Stelle f und die Annäherung aus c) mit Geogebra dar und berechne die durchschnittliche Abweichung von f und der Annäherungsfunktion.)
| AFB III | Kompetenzen K2 K5 K4 | Bearbeitungszeit 30 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
BPE 17.3 Baumdiagramm, Vierfeldertafel, Additionssatz und Bedingte Wahrscheinlichkeit
Aufgabe 40 Kugeln hinzufügen 𝕃
In einer Schüssel sind 20 rote und 10 gelbe Kugeln. Es werden mit einem Zug zwei Kugeln gezogen.
Wie viele blaue Kugeln müssen dazugegeben werden, damit die Wahrscheinlichkeit, zwei gleichfarbige Kugeln zu bekommen,
a) genau \(\frac{70}{183}\) ist? b) höchstens 0,4 ist? c) mindestens 0,5 ist?
| AFB III | Kompetenzen K2 K5 | Bearbeitungszeit k.A. |
| Quelle Beckstette, Glende, Grasemann, Haasis, Kolupa, Widmann | Lizenz CC BY-SA | |
Aufgabe 40 Stochastische Unabhängigkeit Wahrscheinlichkeiten 𝕃
In einer Urne befinden sich 14 durchnummerierte Kugeln. Eine Kugel wird zufällig gezogen. Die Ergebnismenge ist \(\Omega = \lbrace 1, 2, 3, ..., 12, 13, 14 \rbrace \).
- Gib ein Ereignis E an mit Wahrscheinlichkeit \(P(E)=\frac{1}{7}\).
- Begründe, warum zwei Ereignisse F und G mit \(P(F)=P(G)=0{,}8\) stets stochastisch abhängig sind.
| AFB III | Kompetenzen K2 K4 K5 | Bearbeitungszeit k.A. |
| Quelle Niklas Wunder | Lizenz CC BY-SA | |
Aufgabe 41 Kombinatorik 𝕃
 Fünf zehnseitige Würfel (mit den Zahlen 1–10) werden gleichzeitig in einem Würfelbecher geworfen. Für jeden Würfel beträgt die Wahrscheinlichkeit für jede Augenzahl 10%.
Fünf zehnseitige Würfel (mit den Zahlen 1–10) werden gleichzeitig in einem Würfelbecher geworfen. Für jeden Würfel beträgt die Wahrscheinlichkeit für jede Augenzahl 10%.
Untersuche, wie viele unterschiedliche Wurfbilder geworfen werden können. (unterschiedlich im Sinne von alle verschieden, zwei gleiche, ..., alle gleich)
Bild: Dietmar Rabich, Würfel, pentagonales Trapezoeder, Ausschnitt, CC BY-SA 4.0
| AFB III | Kompetenzen K2 K5 K6 | Bearbeitungszeit 25 min |
| Quelle Dr. Andreas Dinh | Lizenz CC BY-SA | |
