BPE 10.4 Aufstellen von Funktionstermen

Zuletzt geändert von Holger Engels am 2024/07/22 15:40

K4 K5 Ich kann aus grafisch gegebenen Funktionseigenschaften den Funktionsterm einer allgemeinen Sinus- bzw. Kosinusfunktion bestimmen
K4 K5 Ich kann aus tabellarisch gegebenen Funktionseigenschaften den Funktionsterm einer allgemeinen Sinus- bzw. Kosinusfunktion bestimmen
K4 K5 Ich kann aus verbal gegebenen Funktionseigenschaften den Funktionsterm einer allgemeinen Sinus- bzw. Kosinusfunktion bestimmen

Das Schaubild zeigt die Graphen von einer Sinus- und einer Kosinusfunkion.
Bestimmen Sie jeweils einen passenden Funktionsterm f(x)  bzw. g(x) .

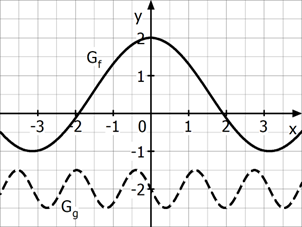
Aufgabe_1.png

Schaubild 1

AFB   IIKompetenzen   K4 K5Bearbeitungszeit   10 min
Quelle   Dennis LöblichLizenz   CC BY-SA

Eine trigonometrische Funktion hat die Amplitude 5 und die Periode 4. Das Schaubild der Funktion hat einen Hochpunkt bei H(0|4).
Bestimmen Sie zwei passende Funktionsterme f(x) bzw. g(x).

AFB   IIKompetenzen   K4 K5Bearbeitungszeit   10 min
Quelle   Dennis LöblichLizenz   CC BY-SA

Von einer allgemeinen cos-Funktion ist bekannt, dass sie im Intervall [0;10] nur an den Stellen x ∈ {1, 3, 7, 9} den Funktionswert 1 hat. Bestimme einen möglichen Funktionsterm.

AFB   IIIKompetenzen   k.A.Bearbeitungszeit   k.A.
Quelle   Holger EngelsLizenz   CC BY-SA

Gib an, wie die Funkion f(x)=-1,5 sin(1,5(x-\pi))+2 mit cos ausgedrückt werden kann.

AFB   IKompetenzen   k.A.Bearbeitungszeit   k.A.
Quelle   Holger EngelsLizenz   CC BY-SA

Kompetenzmatrix und Seitenreflexion

K1K2K3K4K5K6
I000000
II000220
III000000
Bearbeitungszeit gesamt: 20 min
Abdeckung Bildungsplan
Abdeckung Kompetenzen
Abdeckung Anforderungsbereiche
Eignung gemäß Kriterien
Umfang gemäß Mengengerüst