Zum Inhalt springen

Lösung Funktionswert bekannt

Zuletzt geändert von Holger Engels am 2025/10/02 19:47

Zwei Wege führen zum Ziel ..

Rückführung auf den Standard Sinus
Wenn man es nicht auswendig weiß, kann man den Taschenrechner zuhilfe nehmen, um zu ermitteln, dass die Standard Sinusfunktion den Wert 0,5 an der Stelle \(x_1=\frac16\pi\) annimmt. Mithilfe einer Skizze der Standard Sinusfunktion findet man die zweite Stelle in der Periode \(x_2=\frac56\pi\), wo sie wieder diesen Wert annimmt.

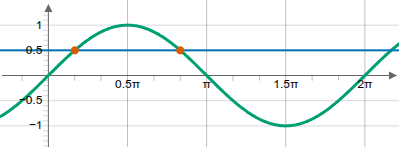
Standard Sinus.png

Die Standard Sinusfunktion nimmt diesen Wert also bei \(\frac{1}{12}\) und \(\frac{5}{12}\) der Periode an. Der (horizontale) Abstand 6 - 2 = 4 entspricht also \(\frac{4}{12}\) der Periode. Die Periodenlänge beträgt demnach p = 12. Der Mittelliniendurchgang ist \(\frac{1}{12}\) links vom ersten Punkt, also an der Stelle x = 1. Damit ergibt sich der Funktionsterm

\[f(x)=\sin(\frac{1}{6}\pi(x-1))\]

Skizze
Skizze.svg
Der Skizze kann man die Mittelliniendurchgänge entnehmen. Daraus ergeben sich Periodenlänge und horizontale Verschiebung.