Zum Inhalt springen

Lösung Lokale und mittlere Änderungsrate

Zuletzt geändert von akukin am 2024/10/20 21:43
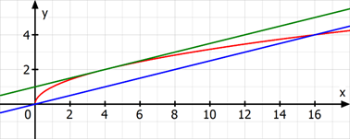
Erwartungshorizont Die betrachtete mittlere Änderungsrate ist gleich der Steigung von g.
Damit gilt für x\in\mathbb{R}^+:\ \ f^\prime\left(x\right)=\frac{1}{4}\ \ \ \Leftrightarrow\ \ \frac{1}{2\sqrt x}=\frac{1}{4}\ \ \ \Leftrightarrow\ \ \ \sqrt x=2\ \ \ \Leftrightarrow\ \ \ x=4
Erläuterung der Lösung 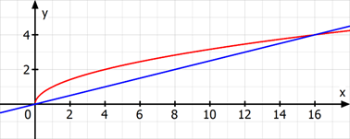WurzelxÄnderungsrate.png Der rote Graph gehört zur Funktion f mit f\left(x\right)=\sqrt x; die blaue Gerade hat die Gleichung y=\frac{1}{4}x.
Die beiden Graphen schneiden sich bei x=0 und x=16, also geht es um das Intervall \left[0;16\right].
Die durchschnittliche Änderungsrate der Funktion f in diesem Intervall ist die Steigung der Sekante, die den Graphen an den Intervallgrenzen schneidet. Man kann erkennen, dass diese Sekante die eingezeichnete Gerade ist. Also ist die durchschnittliche Änderungsrate \frac{1}{4}.
Als Nächstes suchen wir eine Stelle im Intervall, an der die Tangente an den Graphen von f dieselbe Steigung \frac{1}{4} hat, denn die Steigung der Tangente ist ja die lokale Änderungsrate.

Die Funktion f mit f\left(x\right)=\sqrt x=x^\frac{1}{2} leiten wir ab mit der Regel: f\left(x\right)=x^n\ \ \Rightarrow\ \ f^\prime\left(x\right)=nx^{n-1}

f^\prime\left(x\right)=\frac{1}{2}x^{-\frac{1}{2}}

Jetzt müssen wir nur noch dasjenige x\in\left[0;16\right] finden, für das f^\prime\left(x\right)=\frac{1}{4} tatsächlich gilt.

\begin{align} \frac{1}{2}x^{-\frac{1}{2}} &=\frac{1}{4} \quad \mid \cdot2 \\ x^{-\frac{1}{2}} &=\frac{1}{2} \quad \mid ()^2 \\ x^{-1} &=\frac{1}{4} \quad \mid\cdot 4x \quad \text{(oder Kehrwert)} \\ 4&=x \end{align}

Das heißt an der Stelle x=4 ist die lokale Änderungsrate von f gleich der durchschnittlichen Änderungsrate im Intervall \left[0;16\right]. WurzelxÄnderungsrateLösung.png