Tipp Lokale und mittlere Änderungsrate
Zuletzt geändert von akukin am 2024/10/20 19:16
Hinweis 1
Mache dir eine Skizze der Graphen von \(f\) und \(g\), sodass du das beschriebene Intervall gut erkennen kannst. (Tipp: 1 Längeneinheit sollte 0,5cm entsprechen.)
Bestimme die beiden Punkte, an denen sich die Graphen von \(f\) und \(g\) schneiden. Es geht um den Bereich zwischen diesen beiden Punkten.
Zu beantworten sind folgende Fragen:Wie groß ist die durchschnittliche Änderungsrate in diesem Bereich?
Und wo ist die lokale (punktuelle) Änderungsrate genauso groß wie die durchschnittliche?
Hinweis 2
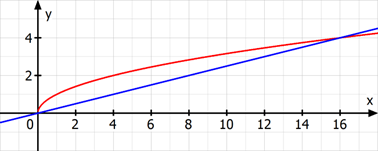
Das beschriebene Intervall ist \(\left[0;16\right]\), denn die beiden Graphen schneiden sich bei \(x=0\) und \(x=16\).
Die durchschnittliche Änderungsrate von \(f\) in diesem Intervall ist (wie immer) die Steigung der Sekante, die den Graphen an den Intervallgrenzen schneidet.Die lokale Änderungsrate von \(f\) an einem Punkt in diesem Intervall ist (wie immer) die Steigung der Tangente, die den Graphen in diesem Punkt berührt.
Hinweis 3
Die gesuchte Sekante ist die gegebene Gerade selbst; ihre Steigung ist \(\frac{1}{4}\).
Gesucht ist also ein Punkt auf dem Graphen von \(f\), an dem die Tangente dieselbe Steigung \(\frac{1}{4}\) hat.