Lösung Fläche zwischen Tiefpunkten
Zuletzt geändert von akukin am 2025/08/14 17:22
Die trigonometrische Funktion ist 2 LE nach oben verschoben. Die Amplitude hat den Wert 2. Die Periode ergibt sich mit \( p=\frac{2\pi}{b}=\frac{2\pi}{\frac{\pi}{2}}=4 \). Damit ergeben sich die Tiefpunkte als Schnittstelle mit der x-Achse bei \( x=3+4*k; k\in\mathbb{R} \). Siehe Skizze.
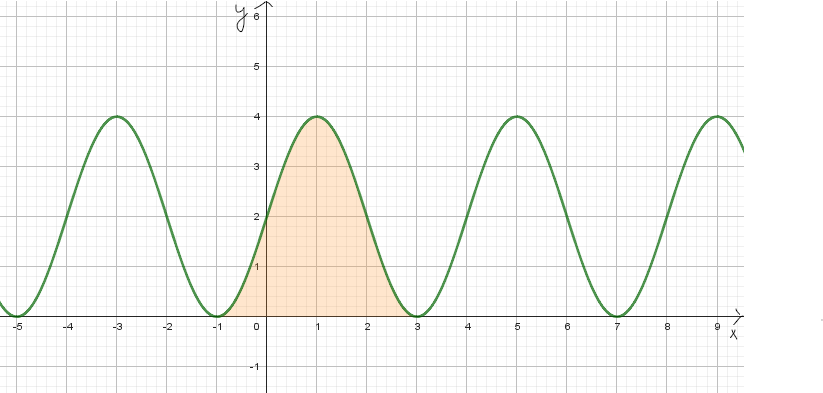
Die gesuchte Fläche berechnet sich also zum Beispiel so:
\[\int_{-1}^3 f(x)dx = \int_{-1}^3 (2+2\sin(\frac{\pi}{2}x))dx = [2x - \frac{4}{\pi}\cos(\frac{\pi}{2}x)]_{-1}^3 =(2*3-\frac{4}{\pi}\cos(\frac{\pi}{2}*3))-(2*(-1)-\frac{4}{\pi}\cos(\frac{\pi}{2}*(-1)))=8\]
Die gesuchte Fläche ist 8 FE groß.
