Lösung Symmetrie und Flächeninhalt
Zuletzt geändert von akukin am 2024/10/20 16:38
Teilaufgabe 1
Erwartungshorizont
Das Polynom \(f\left(x\right)\) enthält ausschließlich Potenzen von \(x\) mit ungeraden ExponentenErläuterung der Lösung
Da es sich um eine Polynomfunktion handelt, kann man sich an den Hochzahlen der Potenzen von \(x\) orientieren:- Kommen ausschließlich ungerade Hochzahlen vor, ist der Graph punktsymmetrisch zum Ursprung.
- Gibt es nur gerade Hochzahlen, ist der Graph achsensymmetrisch zur y-Achse.
- Bei einer Kombination aus geraden und ungeraden Hochzahlen steht fest, dass der Graph weder zum Ursprung noch zur y-Achse symmetrisch ist.
Man könnte die Symmetrie zum Ursprung auch formal beweisen, indem man zeigt, dass für alle \(x\in\mathbb{R}\) gilt:
\(f\left(-x\right)=-f\left(x\right)\)
Bei Polynomfunktionen bietet sich jedoch die erstgenannte Strategie an.
Teilaufgabe 2
Erwartungshorizont
\(f\left(x\right)=0\ \ \ \Leftrightarrow\ \ \ x\cdot\left(x^2-4\right)=0\ \ \ \Leftrightarrow\ \ \ x=-2\ \ \vee\ \ x=0\ \ \vee\ \ x=2\)\(2\cdot\int_{-2}^{0}{f\left(x\right)\mathrm{d} x}=2\cdot\left[\frac{1}{4}x^4-2x^2\right]_{-2}^0=2\cdot\left(0-\left(4-8\right)\right)=8\)
Erläuterung der Lösung
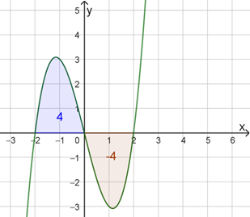
In einer Skizze erkennt man die beiden Teilflächen. Ihren Inhalt kann man mittels Integralrechnung bestimmen. Dazu benötigt man zuerst die Nullstellen, denn diese sind die linken und rechten Grenzen der Teilflächen.
Mit Hilfe des Satzes vom Nullprodukt erhält man die drei Nullstellen:\(f\left(x\right)=0\ \ \ \Leftrightarrow\ \ \ x\cdot\left(x^2-4\right)=0\ \ \ \Leftrightarrow\ \ \ x=-2\ \ \vee\ \ x=0\ \ \vee\ \ x=2\)
Da der Graph symmetrisch zum Ursprung ist, genügt es, eine der beiden Teilflächen zu bestimmen und das Ergebnis zu verdoppeln:
\(A=2\cdot\int_{-2}^{0}{f\left(x\right)\mathrm{d} x}=2\cdot\int_{-2}^{0}{\left(x^3-4x\right)\mathrm{d} x}=2\cdot\left[\frac{1}{4}x^4-2x^2\right]_{-2}^0=2\cdot\left(0-\left(4-8\right)\right)=8\)
Also hat die Gesamtfläche den Inhalt von \(8\) Flächeneinheiten.
