Zum Inhalt springen

Lösung Geraden zeichnen

Version 4.1 von akukin am 2024/10/01 00:21
Erwartungshorizont eingezeichneteGeraden.png
\overrightarrow{OB}+\frac{\left|\overrightarrow{PB}\right|}{\left|\overrightarrow{AP}\right|}\cdot\overrightarrow{AP}
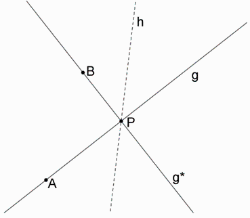
Erläuterung der Lösung eingezeichneteGeraden.png Da sich g und g^\ast in P schneiden und jeweils ein weiterer Punkt gegeben ist (A liegt auf g, B liegt auf g^\ast), können diese beiden Geraden sofort eingezeichnet werden.
Da h die Gerade sein soll, an der g gespiegelt g^\ast ergibt, muss h eine Winkelhalbierende von g und g^\ast sein. (Die andere, um 90° gedrehte Winkelhalbierende wäre auch möglich.)
Mit dem Spiegelpunkt B\prime, der entsteht, wenn B an h gespiegelt wird, ergeben B,P,B^\prime und ein weiterer Punkt auf h eine Raute, deren Diagonale auf h liegt. Addiert man die Vektoren \overrightarrow{PB} und \overrightarrow{PB^\prime}, erhält man also einen Vektor, mit dem man von P entlang h zu einem weiteren Punkt auf h kommt. 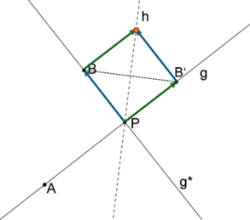Geradenmitspiegelpunkt.png Obwohl B^\prime nicht zur Verfügung steht, kann \overrightarrow{PB^\prime} mit Hilfe von \overrightarrow{AP} ausgedrückt werden, denn beide Vektoren zeigen in dieselbe Richtung, haben jedoch unterschiedliche Längen (Beträge). Mit Hilfe der Beträge \left|\overrightarrow{AP}\right| und \left|\overrightarrow{PB}\right| kann \overrightarrow{AP} jedoch derart verkürzt werden, sodass \overrightarrow{PB^\prime} entsteht. Dazu wird \overrightarrow{AP} zuerst auf die Länge 1 skaliert, indem er durch seinen eigenen Betrag geteilt wird. Mit anderen Worten: Es wird der Einheitsvektor von \overrightarrow{AP} gebildet:
\frac{\overrightarrow{AP}}{\left|\overrightarrow{AP}\right|}
Im Anschluss wird dieser Einheitsvektor mit der Länge von \overrightarrow{PB} multipliziert. (\overrightarrow{PB} und \overrightarrow{PB\prime} haben ja denselben Betrag.)
\frac{\overrightarrow{AP}}{\left|\overrightarrow{AP}\right|}\cdot\left|\overrightarrow{PB}\right| Jetzt haben wir den gesuchten Verbindungsvektor, mit dem wir von P entlang h zu einem weiteren Punkt auf h kommen. Der dazugehörige Ortsvektor des weiteren Punktes auf h lautet: \overrightarrow{OB}+\frac{\left|\overrightarrow{PB}\right|}{\left|\overrightarrow{AP}\right|}\cdot\overrightarrow{AP}