BPE 9.1 Rechtwinkliges Dreieck, Satz des Pythagoras
K4 K5 Ich kann im rechtwinkligen Dreieck die Seiten angeben.
K1 K6 Ich kann den Satz des Pythagoras beweisen.
K4 K5 Ich kann den Satz des Pythagoras als algebraischens Hilfsmittel zur Zeichnung und zur Berechnung von Streckenlängen anwenden.
K4 K5 Ich kann den Satz des Pythagoras als algebraisches Hilfsmittel zur Untersuchung von Orthogonalität (Rechtwinkligkeit) in Figuren und Körpern anwenden.
1 Fehlende Seite berechnen (6 min) 𝕃
Berechne die fehlenden Seitenlängen im rechtwinkligen Dreieck. Runde ggf. auf zwei Nachkommastellen.
| AFB I - K4 K5 | Quelle Christine Müller, Miriam Schneider |
2 Drachen basteln (10 min) 𝕃
Im Herbst bastelt Frida einen Drachen (vgl. Abbildung). Die Kantenlängen a und b sind 30cm und 50cm lang.
Ihr Vater hat einen 110cm langen Holzstab, den er für die Diagonalen des Drachen auseinandersägen könnte. Untersuche, ob dieser Holzstab lang genug ist.
| AFB II - K1 K2 K5 K6 | Quelle Christine Müller, Miriam Schneider |
3 Drachen steigen (10 min) 𝕃
Lieschen hat einen neuen Drachen und geht mit ihm drachensteigen. Sie lässt die Drachenschnur 20m aus. Plötzlich verfängt sich der Drachen in einer hohen Tanne. Lieschen läuft zur Tanne und misst anhand ihrer Schritte eine Entfernung von 18m bis zur Tanne.
Berechne die Höhe der Tanne. Gehe davon aus, dass Lieschen die Drachenschnur auf einer Höhe von 1,30m hält. Fertige eine geeignete Skizze an.
| AFB II - K2 K3 K4 K5 | Quelle Christine Müller, Miriam Schneider |
4 Zaubertrick (12 min) 𝕋 𝕃
Magier „Verschwindibus“ möchte einen Verschwinde-Trick vorführen. Sein 25cm langer Zauberstab soll in seinem Zylinder (Durchmesser 15cm) verschwinden.
- Berechne wie hoch sein Zylinder sein muss, damit der Verschwinde-Trick gelingt.
- Bestimme, welche Maße ein Zylinder besitzen müsste, in den ein Zauberstab der Länge 36cm bzw. der Länge \(\sqrt{122}\) cm exakt passt.
| AFB III - K2 K3 K5 | Quelle Christine Müller, Miriam Schneider |
5 Umfang eines Dreiecks (5 min) 𝕃
Berechne den Umfang des Dreiecks \(ABC\) mit \(A(-2|3), B(10|-2), C(1|7)\).
| AFB II - K5 | Quelle Team Mathebrücke | #mathebrücke |
6 Flächeninhalt eines Dreiecks (14 min) 𝕃
Die Punkte \(A(-2|-3), B(7|3)\) und \(C(0|7)\) sind die Ecken eines Dreiecks \(ABC\). Zudem ist der Punkt \(H(4|1)\) gegeben.
- Zeichne das Dreieck \(ABC\) und den Punkt \(H\) in ein Koordinatensystem und zeige durch Rechnung, dass der Punkt \(H\) auf der Seite \(AB\) liegt.
- Prüfe mit Hilfe des Satzes des Pythagoras, ob das Dreieck \(BCH\) rechtwinklig ist.
- Berechne die Fläche des Dreiecks \(ABC\).
| AFB III - K4 K5 | Quelle Mathebrücke | #mathebrücke |
7 Rechtwinkliges Dreieck (8 min) 𝕃
Die Punkte \(A(2|2), B(0,5|1)\) und \(C(4|-1)\) bilden ein Dreieck.
Zeige, dass dieses Dreieck rechtwinklig ist.
| AFB III - K4 K5 | Quelle Mathebrücke | #mathebrücke |
8 Dreiecksseiten (10 min) 𝕃
Begründe, dass in einem rechtwinkligen Dreieck die Summe der Kathetenlängen größer als die Hypotenusenlänge ist.
| AFB III - K1 K6 | Quelle Mathebrücke | #mathebrücke |
9 Pythagoras herleiten 1 (10 min) 𝕃
Hier siehst du zwei gleich große Quadrate. Das schraffierte Dreieck ist ein rechtwinkliges Dreieck mit den Katheten a und b. Begründe anhand der beiden Bilder, warum a² und b² zusammen so groß ist wie c².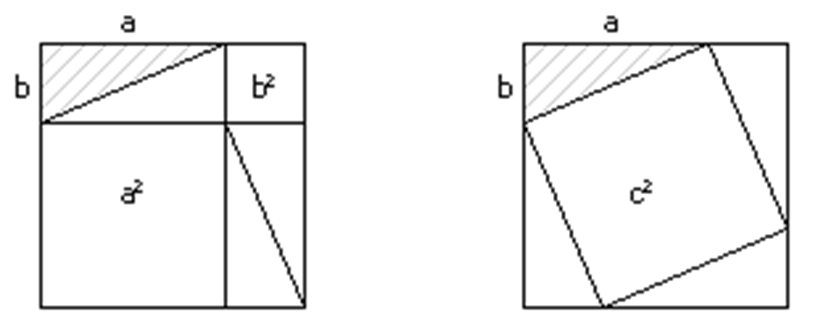
| AFB III - K1 K6 | Quelle Helmut Diehl |
10 Pythagoras herleiten 2 (10 min) 𝕋 𝕃
Hier siehst du ein Quadrat. Das schraffierte Dreieck ist ein rechtwinkliges Dreieck mit den Katheten a und b. Die Hypotenuse c ist die Seite des äußeren Quadrates.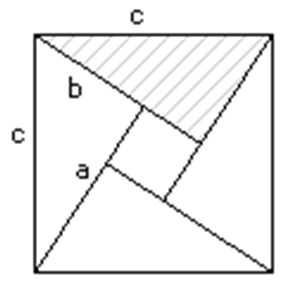
Das Quadrat ist in vier gleiche Dreiecke und ein klines inneres Quadrat zerlegt. Zeige, dass c²=a²+b² gilt, indem du die Flächen der fünf Teile zusammenzählst und ein wenig rechnest.
| AFB III - K2 K5 | Quelle Helmut Diehl |
11 Leiter (12 min) 𝕃
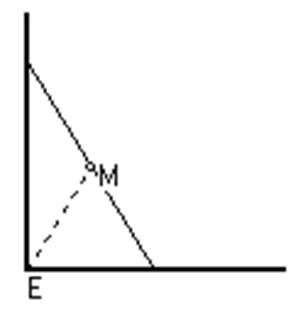
Eine 5m lange Leiter lehnt an einer senkrechten Wand. Wenn du das untere Ende ganz an die Wand schiebst, steht die Leiter senkrecht an der Wand. Wenn man das untere Ende wegzieht, rutscht das obere Ende an der Wand hinunter.
Felix stellt fest:
Die Mitte der Leiter ist von der Ecke unten immer gleich weit entfernt.
Erkläre, weshalb dies gilt. Beschreibe, auf welcher Bahn sich die Mitte der Leiter demnach bewegt.
| AFB III - K1 K6 K5 | Quelle Helmut Diehl |
