Zum Inhalt springen

Lösung Aufgabe 3

Version 6.1 von akukin am 2025/01/23 22:32

Teilaufgabe a)

Erwartungshorizont (offiziell) LösungGraphAufgabe3a).png
Erläuterung der Lösung Aufgabenstellung

Zeichne den Graphen von \(k\) für \(0\le t\le10\).

Lösung
Ein Graph kann mittels Wertetabelle gezeichnet werden, die mit dem Taschenrechner erzeugt wird. LösungGraphAufgabe3a).png

Teilaufgabe b)

Erwartungshorizont (offiziell) \(t\approx2\)
Erläuterung der Lösung Aufgabenstellung

Gib anhand der Zeichnung näherungsweise den Zeitpunkt an, zu welchem die Konzentration am stärksten abnimmt.

Lösung
Gesucht ist die Zeit, an der der Graph von \(k\) am steilsten bergab geht.
\(t\approx2\)

Teilaufgabe c)

Erwartungshorizont (offiziell) \(k^\prime\left(7\right)<0\): Bei \(t=7\) liegt eine negative Steigung des Graphen vor.

\(k^{\prime\prime}\left(7\right)>0\): Bei \(t=7\) ist der Graph linksgekrümmt.

Interpretation:
7 Stunden nach der Einnahme nimmt die Konzentration des Medikamentes im Blut ab und die Geschwindigkeit der Abnahme sinkt.
Erläuterung der Lösung Aufgabenstellung

Es gilt \(k^\prime(7)<0\) und \(k^{\prime\prime}(7)>0\). Erläutere die Bedeutung dieser beiden Aussagen hinsichtlich des Verlaufs des Graphen von \(k\). Interpretiere diese beiden Aussagen im Sachzusammenhang.

Lösung
\(k^\prime\left(7\right)<0\): Bei \(t=7\) liegt eine negative Steigung des Graphen vor.

\(k^{\prime\prime}\left(7\right)>0\): Bei \(t=7\) ist der Graph linksgekrümmt.

Interpretation:
7 Stunden nach der Einnahme nimmt die Konzentration des Medikamentes im Blut ab, da die erste Ableitung negativ ist, und die Geschwindigkeit der Abnahme sinkt, da die Änderungsrate der ersten Ableitung, also die zweite Ableitung, positiv ist.

Teilaufgabe d)

Erwartungshorizont (offiziell)

Näherung mit WTR: \(t_1\approx0,75; \ t_2\approx3,66\)

Hinweis: Eine grafische Ermittlung der Zeitpunkte ist ebenfalls zulässig.
Innerhalb der den genannten Zeitpunkten folgenden Stunde verringert sich die Konzentration näherungsweise um 1 \(\frac{\mathrm{mg}}{\mathrm{l}}\).
Erläuterung der Lösung Aufgabenstellung

Ermittle näherungsweise eine Lösung der Gleichung \(k(t)-k(t+1)=1\) und interpretiere diese Lösung im Sachzusammenhang.

Lösung

Gesucht ist ein Zeitpunkt, ab dem innerhalb von einer Stunde die Konzentration um \(1 \frac{\mathrm{mg}}{\mathrm{l}}\) abnimmt.

Man kann mit dem Geodreieck den Graphen abgehen und überprüfen, in welchem horizontalen 1-cm-Intervall der Graph um 1 cm absinkt (grüne Dreiecke).

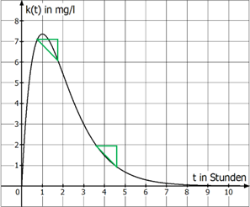
LösungAufgabe3d).png

Die obige Gleichung kann aber auch mit Hilfe des Taschenrechners näherungsweise gelöst werden (Wertetabelle):
Näherung mit WTR: \(t_1\approx0,75; \ t_2\approx3,66\)
Interpretation:
Innerhalb der den genannten Zeitpunkten folgenden Stunde verringert sich die Konzentration näherungsweise um \(1 \frac{\mathrm{mg}}{\mathrm{l}}\).