\(f(x)=(x+2)^2-3\)
a) Bei dem Funktionsgraphen handelt es sich um eine verschobene Normalparabel mit Scheitelpunkt \(S(-2|-3)\).
Ein geeignetes Intervall wäre zum Beispiel \(-5 \leq x \leq 1 \) (man könnte auch ein anderes Intervall nehmen doch mit Blick auf Teilaufgabe c) ist es sinnvoll, wenn der Punkt \(P_2(1|6) \) in der Skizze enthalten ist).

b) \(f(-3)=(-3+2)^2-3=-2\)
\(f(1)=(1+2)^2-3=6\)
c) 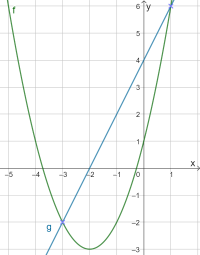
d) Die Steigung lässt sich mit Hilfe eines Steigungsdreieckes (bzw. über \(m=\frac{y_2-y_1}{x_2-x_1}\)) bestimmen. Dabei eignet es sich, für das Steigungsdreieck die Punkte \(P_1\) und \(P_2\) zu wählen, da diese bekannt sind und so kein Fehler beim Ablesen entstehen kann:
Einsetzen von \(m=2\) und \(P_2(1|6)\) in \(y=mx+b\):
Somit lautet die Gleichung der Geraden
\(g: y=2x+4 \quad (g(x)=2x+4)\)
e)
Für \(x>2\) (\(x \in ]2;\infty[\)) verläuft die Gerade \(g\) oberhalb der x-Achse.
f) Da \(h\) senkrecht auf \(g\) steht, gilt für deren Steigungen \(m_h\cdot m_g =-1\). Mit \(m_g=2\) ergibt sich:
Somit lautet die Geradengleichung \(h(x)=-\frac{1}{2}x+b\). Da \(h\) einen gemeinsamen Punkt mit \(f\) und \(g\) haben soll, setzen wir \(f\) und \(g\) gleich, um deren Schnittpunkt(e) rauszubekommen, womit sich dann \(b\) bestimmen lässt.
