BPE 3.3 Aufstellen von Funktionstermen

Zuletzt geändert von Holger Engels am 2024/12/17 20:07

Inhalt

AFB I Änderungen sind bemerkenswert Produktdarstellung
AFB II Parabel aus zwei Punktproben mit Zusatzinformation Parabel aus drei Punktproben Fragestellungen zu einer Wertetabelle Bedingungen zum Aufstellen Funktionstermbestimmung bei Polynomfunktionen

K5 Ich kann den passenden Ansatz für die Ermittlung eines Funktionsterms anhand gegebener Bedingungen bestimmen
K4 K5 Ich kann den Funktionsterm anhand verbal gegebener Bedingungen aufstellen
K4 K5 Ich kann den Funktionsterm anhand tabellarisch gegebener Bedingungen aufstellen
K4 K5 Ich kann den Funktionsterm anhand eines Schaubilds aufstellen

Aufgabe 1 Änderungen sind bemerkenswert 𝕃

Liegen die Punkte auf einer Parabel?

0	1	2
1	1	1
1	3	5

AFB I	Kompetenzen K2 K4 K5	Bearbeitungszeit k.A.
Quelle Martin Rathgeb, Martin Stern		Lizenz CC BY-SA

Aufgabe 2 Parabel aus zwei Punktproben mit Zusatzinformation 𝕃

Scheitel(punkts)form. Bestimme aus folgenden Wertetabellen (je zwei Wertepaare) mit Zusatzinformation jeweils die quadratische Funktion.

	1	3
	2	1
	0	0
	2	2
	2	1

AFB II	Kompetenzen K2 K4 K5	Bearbeitungszeit k.A.
Quelle Martin Rathgeb, Martin Stern		Lizenz CC BY-SA

Aufgabe 3 Parabel aus drei Punktproben

Haupt-, Scheitel(punkts)-, Produktform. Bestimme aus folgenden Wertetabellen (je drei Wertepaare) jeweils die quadratische Funktion.

1	2	3
0	0	1
3	1	3
-2	1	2
-2	0	-2

AFB II	Kompetenzen K2 K4 K5	Bearbeitungszeit k.A.
Quelle Martin Rathgeb, Martin Stern		Lizenz CC BY-SA

Aufgabe 4 Produktdarstellung 𝕋 𝕃

Gegeben ist das Schaubild der Funktion f mit f(x)=0,2(x-1)(x+2)(x-4) .
Triff mindestens vier Aussagen über das Schaubild und begründe, weshalb diese ausreichen, um einen Ansatz für die Ermittlung eines Funktionsterms zu bestimmen.
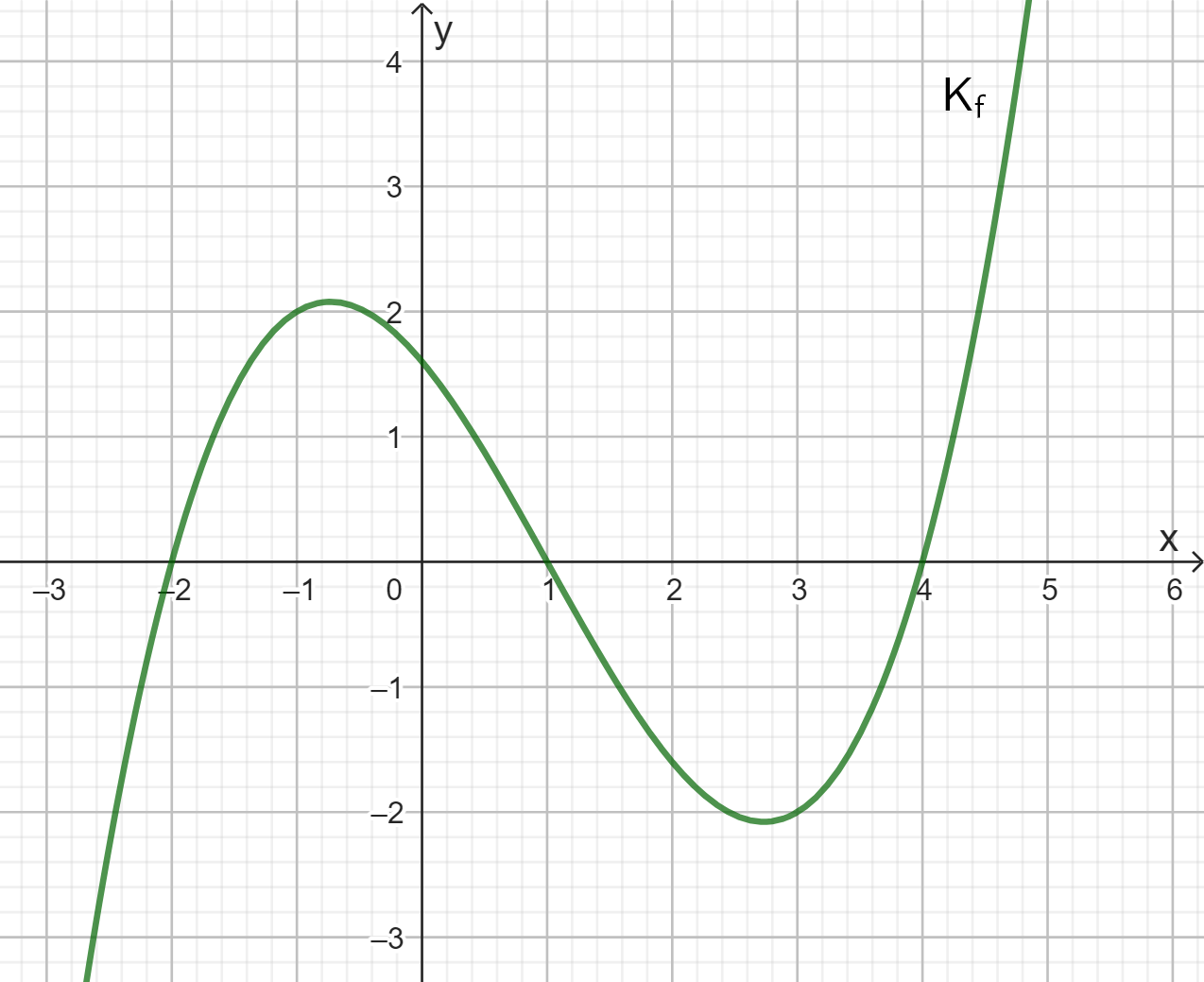
Schaubild Aufgabe 1.png

AFB I	Kompetenzen K1 K4 K5	Bearbeitungszeit 5 min
Quelle Miriam Erdmann		Lizenz k.A.

Aufgabe 5 Fragestellungen zu einer Wertetabelle

Gegeben ist der Ausschnitt einer Wertetabelle einer Funktion 3. Grades

	-4	-3,5	-3	-2,5	-2	-1,5	-1	-0,5	0
	-3	-0,625	0	-0,375	-1	-1,125	0	3,125	9

Begründe, dass folgende Aussagen wahr sind:
1. Der Graph der Funktion f hat eine doppelte Nullstelle bei -3.
2. Der Graph der Funktion f hat eine einfache Nullstelle bei -1.
3. Der Graph verläuft vom dritten in den ersten Quadranten.
4. Der Punkt R(1|-8) liegt nicht auf dem Graphen der Funktion f.
Ermittle die Funktionsgleichung von f in der Produktform.

AFB II	Kompetenzen K1 K4 K5 K6	Bearbeitungszeit 20 min
Quelle Martina Wagner, Dirk Tebbe, Martin Rathgeb, Martin Stern		Lizenz CC BY-SA

Aufgabe 6 Bedingungen zum Aufstellen 𝕃

Gegeben sind die Schaubilder dreier Funktionen. Gib jeweils den Grad der zugehörigen Funktion sowie notwendige Bedingungen zum Aufstellen des Funktionsterms an.
Bedingungen f.svg Bedingungen g.svg Bedingungen h.svg

AFB II	Kompetenzen K4 K5	Bearbeitungszeit 7 min
Quelle Miriam Erdmann		Lizenz CC BY-SA

Aufgabe 7 Funktionstermbestimmung bei Polynomfunktionen 𝕃

Bestimme einen Funktionsterm einer Polynomfunktion mit den folgenden Eigenschaften:
a) Das Schaubild hat bei x=1 eine sechsfache Nullstelle und schneidet die y-Achse an der Stelle 4.
b) Das Schaubild hat bei x=-4 eine einfache, bei x=-2 eine doppelte und bei x=3 eine dreifache Nullstelle. Außerdem schneidet es die y-Achse bei y=27 .
c) Das Schaubild ist symmetrisch zur y-Achse und geht durch P(2|10) und Q(0|0) .
d) Das Schaubild verläuft punktsymmetrisch zum Ursprung. Es hat eine einfache Nullstelle bei x=4 und eine doppelte Nullstelle bei x=-3 .