Inhalt
K6 K4 Ich kann Polynomfunktionen und ihre Eigenschaften in einem gegebenen Sachzusammenhang deuten
K4 K5 Ich kann Polynomfunktionen zur Darstellung einfacher Optimierungsprobleme ermitteln
K4 K6 K5 Ich kann Wertetabellen, Funktionsgraphen und Funktionsterme zur Lösung von Optimierungsproblemen interpretieren
Aufgabe 1 Heißluftballons (gAN)
Fahrt eines Heißluftballons
Das Schaubild stellt die Fahrt eines Heißluftballons dar.
Die Geschwindigkeit (in m/min) ist auf der y-Achse in Abhängigkeit der vergangenen Zeit auf der x-Achse (in min) abgetragen.
Anmerkung: Wenn der Wind sich dreht, kann der Ballon auch rückwärts fahren.
- Welche Bedeutung haben die negativen Funktionswerte?
- Welche Aussagen kann man über den zur Fahrt gehörenden Funktionsterm treffen?
- Wir wollen nun wissen, zu welchen Zeitpunkten der Ballon weder vorwärts noch rückwärts gefahren ist.
Die folgende Funktion f mit D=[0;60], beschreibt näherungsweise die Geschwindigkeit des Ballons:
| AFB II | Kompetenzen K6 K1 K4 | Bearbeitungszeit 7 min |
| Quelle k.A. | Lizenz CC BY-SA | |
Aufgabe 2 Die optimale Geschenkschachtel 𝕋 𝕃
Für ein Geburtstagsgeschenk möchtest du eine Schachtel mit möglichst großem Volumen basteln.
Dafür hast du zwei schöne grüne Kartons im DIN A4-Format (einen für die Schachtel und einen für den Deckel) besorgt.
Erläutere dein Vorgehen und ermittle die Maße, die du für diese ideale Geschenkschachtel erhälst.
| AFB III | Kompetenzen K4 K5 | Bearbeitungszeit 15 min |
| Quelle Frauke Beckstette; Kim Fujan | Lizenz CC BY-SA | |
Aufgabe 3 Kommode im Dachzimmer 𝕋 𝕃
Kay bezieht ein neues Zimmer im Dachgeschoss. Um möglichst viel Stauraum zu schaffen, soll in dem farbig markierten Bereich mit Dachschräge eine möglichst große Kommode aufgestellt werden. Welche Höhe und Tiefe sollte die 2 m breite Kommode dann haben?
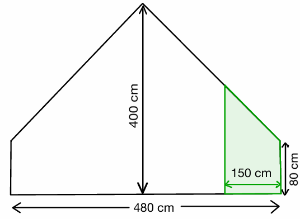
| AFB III | Kompetenzen K4 K5 | Bearbeitungszeit 8 min |
| Quelle Frauke Beckstette; Kim Fujan | Lizenz CC BY-SA | |
Aufgabe 4 Freizeitbad 𝕃
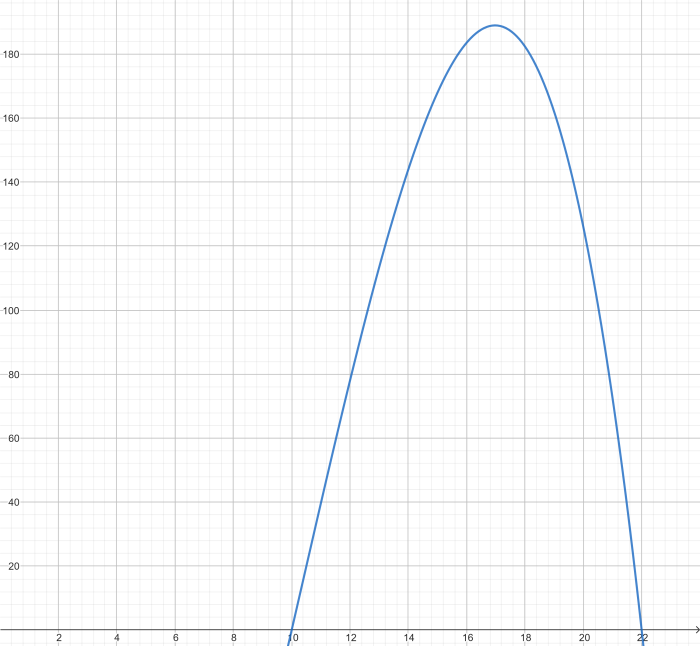
Die Besucherzahlen eines Freizeitbades können zwischen 10:00 Uhr und 22:00 Uhr näherungsweise durch die Funktion in h beschrieben werden.
- Weise rechnerisch nach, dass sowohl um 10:00 Uhr als auch um 22:00 Uhr keine Besucher im Freizeitbad sind.
- Berechne wie viele Besucher 3h vor Badschluss noch im Freizeitbad sind.
- Zu welcher Zeit sind die meisten Besucher im Bad und wie viele sind das? (graphische Lösung)
- Sind mehr als 100 Besucher im Freizeitbad muss eine zusätzliche Schwimmaufsicht gestellt werden. Veranschauliche den Zeitraum, den das betrifft im gegebenen Schaubild und gib den Zeitraum näherungsweise an.
- Beschreibe wie man diesen Zeitraum rechnerisch ermitteln könnte ohne ihn explizit zu berechnen.
| AFB II | Kompetenzen K4 K5 K6 | Bearbeitungszeit 6 min |
| Quelle Frauke Beckstette; Kim Fujan | Lizenz CC BY-SA | |
Kompetenzmatrix und Seitenreflexion
| K1 | K2 | K3 | K4 | K5 | K6 | |
|---|---|---|---|---|---|---|
| I | 0 | 0 | 0 | 0 | 0 | 0 |
| II | 1 | 0 | 0 | 2 | 1 | 2 |
| III | 0 | 0 | 0 | 2 | 2 | 0 |
| Abdeckung Bildungsplan | ||
|---|---|---|
| Abdeckung Kompetenzen | ||
| Abdeckung Anforderungsbereiche | ||
| Eignung gemäß Kriterien | ||
| Umfang gemäß Mengengerüst |