Zum Inhalt springen

Lösung Berechnungen am Quader

Version 26.2 von Holger Engels am 2024/01/30 20:57
  1. Der Punkt ist der Mittelpunkt der Strecke \overrightarrow{OC}

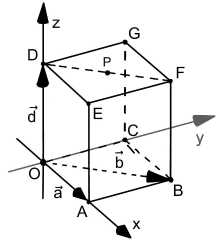
  2. Quadervektorenlösung.jpg

  3. Es gilt \vec{b}\circ \overrightarrow{OP}= \vec{b}\circ \Bigl(\frac{1}{2}\vec{b}+ \vec{d}\Bigl) = \frac{1}{2} \cdot \Bigl(\vec{b}+\vec{b}\Bigl)+\vec{b} \circ \vec{d}.
    Da die Vektoren \vec{b} und \vec{d} senkrecht zu einander stehen, ist deren Skalarprodukt 0 und somit \vec{b}\circ \overrightarrow{OP}= \frac{1}{2} \cdot \Bigl(\vec{b}+\vec{b}\Bigl)+0= \frac{1}{2} \cdot |\vec{b}|^2.
    Damit hängt die Länge des Vektors \vec{b}nur von der Seitenlänge der Grundfläche ab.