BPE 10.2 Transformationen
Inhalt
K6 Ich kann anhand von Funktionstermen beschreiben, wie der Graph einer allgemeinen Sinus- bzw. Kosinusfunktion mittels Transformationen – unter Berücksichtigung der Reihenfolge – aus einer Grundfunktion entsteht
K6 Ich kann anhand von Funktionsgraphen beschreiben, wie der Graph einer allgemeinen Sinus- bzw. Kosinusfunktion mittels Transformationen – unter Berücksichtigung der Reihenfolge – aus einer Grundfunktion entsteht
K4 K5 Ich kann zu einer verbal gegebenen Transformation den zugehörigen Funktionsterm angeben
K4 K5 Ich kann zu einer grafisch gegebenen Transformation den zugehörigen Funktionsterm angeben
(Im grundlegenden Anforderungsniveau wird horizontal nur entweder veschoben oder gestreckt. Im erhöhten Anforderungsniveau werden auch Kombinationen dieser beiden Transformationen betrachtet)
1 Transformationen (8 min) 𝕃
Führe folgende Transformationen mit einer Standard Sinusfunktion durch:
- Streckung in x-Richtung um den Faktor 2, anschließend Verschiebung um \(\pi\) nach rechts.
- Verschiebung um \(\pi\) nach rechts, anschließend Streckung in x-Richtung um den Faktor 2.
| Einordnung AFB I - K4 K5 | Quelle Holger Engels |
2 Periode gegeben (8 min) 𝕃
Strecke die Standard Sinusfunktion so, dass ihre Periodenlänge 4 beträgt.
| Einordnung AFB I - K4 K5 | Quelle Holger Engels |
3 TP und HP (4 min) 𝕃
Eine cos-Funktion hat einen TP bei T(1|1) und einen HP bei H(5|5). Gib einen möglichen Funktionsterm an und erläutere, warum es zu dieser Aufgabenstellung keine eindeutige Lösung gibt.
| Einordnung AFB I - K4 K5 | Quelle Holger Engels |
4 Mittellinie (4 min) 𝕋 𝕃
Eine trigonometrische Funktion mit dem Wertebereich [1;5] schneidet die Gerade \(y=3\) an der Stelle \(x=1\) und das nächste mal an der Stelle \(x=4\). Bestimme den Funktionsterm.
| Einordnung AFB I - K4 K5 | Quelle KMap |
5 Tiefpunkte (4 min) 𝕋 𝕃
Zwei aufeinander folgende Tiefpunkt einer trigonometrischen Funktion liegen bei T(1∣1) und T(6∣1). Die Hochpunkte der Funktion liegen auf der Geraden \(y=5\). Bestimme einen passenden Funktionsterm.
| Einordnung AFB I - K4 K5 | Quelle KMap |
6 Takt (4 min)
Eine sin-Funktion schwingt im 4-Sekunden Takt zwischen -1 und 3. Gib einen möglichen Funktionsterm an!
| Einordnung AFB I - K4 K5 | Quelle Holger Engels |
7 Transformationsschritte (3 min) 𝕃
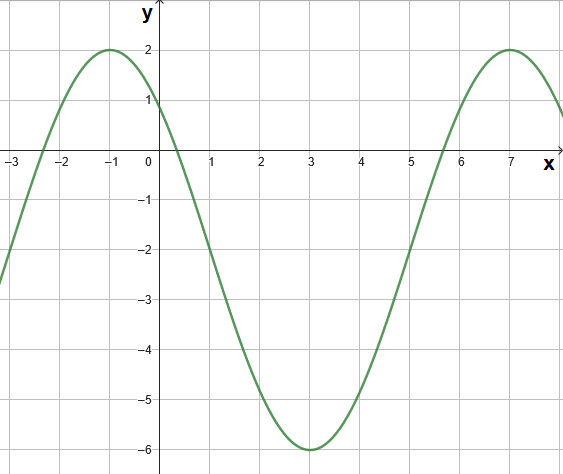
Geben Sie für jede der folgenden Funktionsterme die Transformationsschritte an, die dessen Graph in den unten dargestellten Funktionsgraph überführen.
- \(f(x)=\cos(x)-0,5\)
- \(f(x)=\sin(x)-\frac{\pi}{2} \)
- \(f(x)=-4\sin(x) \)
| Einordnung AFB I - K6 | Quelle kickoff |
8 Aus Wertetabelle (2 min) 𝕃
Ermittle anhand der Tabelle die Amplitude, Periode und Gleichung der trigonometrischen Funktion g. Beschreibe wie g aus der Grundfunktion \(f(x)=sin(x)\) hervorgeht.
| x | 0 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
|---|---|---|---|---|---|---|---|---|
| f(x) | 0 | 1,41 | 2,0 | 1,41 | 0 | -1,41 | -2,0 | -1,41 |
| Einordnung AFB II - K4 K5 K6 | Quelle Dirk Tebbe, Corinne Blaumeiser |
Kompetenzmatrix und Seitenreflexion
| K1 | K2 | K3 | K4 | K5 | K6 | |
|---|---|---|---|---|---|---|
| I | 0 | 0 | 0 | 6 | 6 | 1 |
| II | 0 | 0 | 0 | 1 | 1 | 1 |
| III | 0 | 0 | 0 | 0 | 0 | 0 |
| Abdeckung Bildungsplan | ||
|---|---|---|
| Abdeckung Kompetenzen | ||
| Abdeckung Anforderungsbereiche | ||
| Eignung gemäß Kriterien | ||
| Umfang gemäß Mengengerüst |