Zum Inhalt springen

BPE 16 Einheitsübergreifend

Version 14.1 von Holger Engels am 2024/01/06 15:39

Das Gleichungssystem

\begin{align*} I &\quad -x + y =&-3 \\ II &\quad 2x - 2y =&6 \end{align*}

mit x,y \in \mathbb{R}  hat unendlich viele Lösungen.

  1. Stelle diese Lösungen in einem Koordinatensystem grafisch dar. Gib die Lösung mit y=1 an.

Im gegebenen Gleichungssystem wird die Gleichung II durch die folgende Gleichung mit a,b \in \mathbb{R}  ersetzt:

II^* \quad a \cdot x - 3y = b

  1. Gib einen Wert von a und einen Wert von b an, für die das aus I und II^* bestehende Gleichungssystem keine Lösung hat. Begründe deine Angabe.

#iqb

AFB   k.A.Kompetenzen   K1 K2 K4 K5Bearbeitungszeit   k.A.
Quelle   IQBLizenz   k.A.

Gegeben sind die Punkte A(5|-5|12), B(5|5|12) und C(-5|5|12).

  1. Zeige, dass das Dreieck ABC gleichschenklig ist.
  2. Begründe, dass A, B und C Eckpunkte eines Quadrats sein können, und gib die Koordinaten des vierten Eckpunkts D dieses Quadrates an.

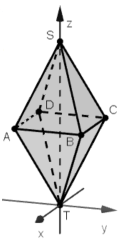Doppelpyramide.pngIm Folgenden wird die rechts abgebildete Doppelpyramide betrachtet. Die beiden Teilpyramiden ABCDS
und ABCDTsind gleich hoch. Der Punkt T liegt im Koordinatenursprung, der Punkt Sebenfalls auf der z-Achse.

Die Seitenfläche BCT liegt in einer Ebene E.

  1. Bestimme eine Gleichung von Ein Koordinatenform. (zur Kontrolle: 12y-5z = 0)
  2. Bestimme die Größe des Winkels, den die Seitenfläche BCT mit der Fläche ABCD einschließt.

E gehört zur Schar der Ebenen E_k: ky-5z = 5k - 60 mit k \in \mathbb{R}.

  1. Alle Ebenen der Schar schneiden sich in einer Gerade. Weise nach, dass die Kante \overline{BC} auf dieser Gerade liegt.
  2. Ermittle diejenigen Werte von k, für die E_k mit der Seitenfläche ADS mindestens einen Punkt gemeinsam hat.
  3. Die Seitenfläche ADT liegt in der Ebene F. Gib einen Normalenvektor von F an und begründe deine Angabe, ohne die Koordinaten von A und D zu verwenden. Bestimme denjenigen Wert von k, für den E_k senkrecht zu F steht.
  4. Die Doppelpyramide wird so um die x-Achse gedreht, dass die bisher mit BCT bezeichnete Seitenfläche in der xy-Ebene liegt und der bisher mit S bezeichnete Punkt eine positive y-Koordinate hat. Bestimme diese y-Koordinate und veranschauliche dein Vorgehen durch eine Skizze.

#iqb

AFB   k.A.Kompetenzen   K1 K2 K4 K5 K6Bearbeitungszeit   k.A.
Quelle   IQBLizenz   k.A.

Abb.1.PNGFür k \in \mathbb{R} mit 0<k\leq 6 werden die Pyramiden ABCD_k mit A(0|0|0), B(4|0|0), C(0|4|0) und D_k(0|0|k) betrachtet (vgl. Abbildung 1).

  1. Begründe, dass das Dreieck BCD_k gleichschenklig ist.
  2. Der Mittelpunkt der Strecke \overline{BC} ist M(2|2|0). Begründe, dass |\overline{MD_k}|= \Bigg|\left(\begin{array}{c} -2 \\ -2 \\ k \end{array}\right) \Bigg| die Länge einer Höhe des Dreiecks BCD_k ist. Bestimme den Flächeninhalt des Dreiecks BCD_k.

Für jeden Wert von k liegt die Seitenfläche BCD_k in der Ebene L_k.

  1. Bestimme eine Gleichung von L_k in Koordinatenform. (zur Kontrolle: x_1+x_2+\frac{4}{k}\cdot x_3 =4)

#iqb

AFB   k.A.Kompetenzen   K1 K2 K4 K5 K6Bearbeitungszeit   k.A.
Quelle   IQBLizenz   k.A.