1 Glücksrad (20 min) 𝕃
Ein Glücksrad mit einem roten Gewinnbereich von einem Viertel wird so gedreht, dass es in einer völlig zufälligen Position zum Stillstand kommt. Einen Beobachter interessiert, wie groß der Abstand der Halteposition (grünes Dreieck in der Skizze) zum Gewinnbereich ist. Er misst den Abstand in Grad.
So ist der Abstand z.B. 0°, falls das Glücksrad im Gewinnbereich zum Stillstand kommt und 90°, falls es nach einem Drittel oder zwei Dritteln des Verlustbereichs zum Stillstand kommt.
Bestimme mit Hilfe einer geeigneten Zeichnung den Erwartungswert dieses Abstands bei einmaliger Drehung des Glücksrads.
| AFB II - K2 K4 K5 | Quelle Dr. Andreas Dinh | #problemlösen |
2 Tetraeder (k.A.) 𝕃
Die vier Seiten eines regelmäßigen Tetraeders sind mit den Zahlen 1, 2, 3 und 4 durchnummeriert. Das Teraeder wird fünfmal geworfen.
- Gib im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term \(\left(\frac{3}{4}\right)^5\) berechnet werden kann, und begründe deine Angabe.
- Gib einen Term an, mit dem die Wahrscheinlichkeit dafür berechnet werden kann, dass jede Zahl mindestens einmal erzielt wird.
| AFB k.A. - K1 K2 K3 K4 K6 | Quelle IQB | #iqb |
3 Kugeln und Würfel (k.A.) 𝕃
In einen leeren Behälter werden drei Kugeln gelegt. Dabei wird die Farbe jeder Kugel durch Werfen eines Würfels festgelegt, dessen Seiten mit den Zahlen 1 bis 6 durchnummeriert sind: Wird die „1“ oder die „2“ erzielt, wird eine gelbe Kugel gewählt, sonst eine schwarze.
- Weise rechnerisch nach, dass die Wahrscheinlichkeit dafür, dass sich nun mindestens zwei schwarze Kugeln im Behälter befinden, \(\frac{20}{27}\) beträgt.
- Aus dem Behälter werden zwei der drei Kugeln zufällig entnommen. Ermittle die Wahrscheinlichkeit dafür, dass beide entnommenen Kugeln schwarz sind.
| AFB k.A. - K1 K2 K3 K5 K6 | Quelle IQB | #iqb |
4 Glücksradiqb (k.A.) 𝕃
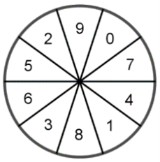
Die Sektoren des abgebildeten Glücksrads sind gleich groß und mit den Zahlen von 0 bis 9 durchnummeriert.
- Das Glücksrad wird zwanzigmal gedreht. Bestimme die Wahrscheinlichkeiten der Ereignisse A und B.
A: „Es wird genau siebenmal eine ungerade Zahl erzielt.“
B: „Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt.“ - Das Glücksrad wird zweimal gedreht. Untersuche, ob die Ereignisse C und D stochastisch unabhängig sind.
C: „Die Summe der erzielten Zahlen ist kleiner als 4.“
D: „Das Produkt der erzielten Zahlen ist 2 oder 3.“ - Mit dem Glücksrad wird ein Spiel durchgeführt. Jeder Spieler darf das Glücksrad beliebig oft drehen. Beendet er das Spiel selbst, bevor er eine „0“ erzielt, so wird ihm die Summe der erzielten Zahlen in Euro ausgezahlt. Erzielt er eine „0“, so ist das Spiel dadurch beendet und es erfolgt keine Auszahlung.
- Ein erster Spieler entscheidet sich vor dem Spiel dafür, das Glücksrad, sofern er keine „0“ erzielt, viermal zu drehen und danach das Spiel zu beenden. Bestimme die Wahrscheinlichkeit dafür, dass er eine Auszahlung erhält.
- Bei einem zweiten Spieler beträgt nach mehrmaligem Drehen des Glücksrads die Summe der erzielten Zahlen 60. Er möchte nun das Spiel entweder sofort beenden oder das Glücksrad genau ein weiteres Mal drehen. Berechne für den Fall, dass sich der Spieler für die weitere Drehung entscheiden sollte, den Erwartungswert für die Auszahlung. Gib eine Empfehlung ab, ob sich der Spieler für das Beenden des Spiels oder für die weitere Drehung entscheiden sollte, und begründe deine Empfehlung.
- Wenn sich ein Spieler vor dem Spiel dafür entscheidet, das Glücksrad, sofern er keine „0“ erzielt, \(n\) -mal zu drehen, dann kann der Erwartungswert für die Auszahlung mit dem Term \(5n\cdot{0,9}^n\) berechnet werden. Beurteile die folgende Aussage:
Es gibt zwei, aber nicht drei aufeinanderfolgende Werte von \( n\) , für die die Erwartungswerte für die Auszahlung übereinstimmen.
- Betrachtet wird ein kleiner zehnseitiger Holzkörper, dessen Seiten mit den Zahlen von 0 bis 9 durchnummeriert sind.
- Bei 80 Würfen wird zwölfmal die „0“ erzielt. Bestimmt man auf dieser Grundlage zur Sicherheitswahrscheinlichkeit 95 % ein Konfidenzintervall für die Wahrscheinlichkeit dafür, bei einem Wurf die „0“ zu erzielen, so ergibt sich als untere Grenze dieses Intervalls näherungsweise 0,09. Begründe, dass die obere Grenze des Konfidenzintervalls größer als 0,1 ist. Beschreibe die Bedeutung des Konfidenzintervalls im Hinblick auf die Annahme, dass beim Werfen des Holzkörpers die „0“ mit einer Wahrscheinlichkeit von 10 % erzielt wird.
- Bestimme die kleinste Anzahl von Würfen, für die Folgendes gilt:
Wenn man bei genau 15 % der Würfe die „0“ erzielt, dann steht dies bei einer Sicherheitswahrscheinlichkeit von 95 % nicht in Einklang mit der Annahme, dass beim Werfen des Holzkörpers die „0“ mit einer Wahrscheinlichkeit von 10 % erzielt wird.
| AFB I, II, III - K1 K2 K3 K4 K5 K6 | Quelle IQB | #iqb |
