BPE 7.1 Punkte und Vektoren
K4 Ich kann Vektoren als Pfeilklassen deuten
K4 K6 Ich kann Vektoren geometrisch als Verschiebung interpretieren
K4 Ich kann geometrische Objekte im dreidimensionalen Koordinatensystem zeichnen
K4 K1 Ich kann das Koordinatensystem nutzen, um geometrische Sachverhalte zu beschreiben
Punkte im Raum
1 Punkte einzeichnen (3 min) 𝕃
Zeichne die Punkte \(A(2|4|2)\) und \(B(-4|1|-1)\) in ein gemeinsames Koordinatensystem. Was fällt auf?
| AFB I - K4 K6 | Quelle Holger Engels | |
| Links Interaktiv | ||
2 Punkte ablesen (4 min) 𝕃
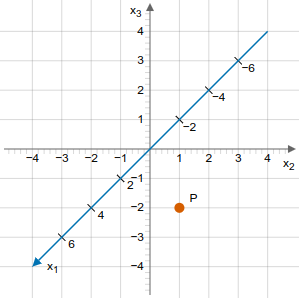 Gib jeweils an, welche Koordinaten der eingezeichnete Punkt haben könnte, wenn eine Koordinate vorgegeben ist.
Gib jeweils an, welche Koordinaten der eingezeichnete Punkt haben könnte, wenn eine Koordinate vorgegeben ist.
| AFB II - K4 | Quelle Holger Engels | |
| Links Interaktiv | ||
3 Zeichenebene (6 min) 𝕃
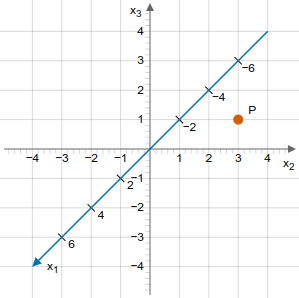 Im Schaubild siehst du den Punkt \(P(2|4|2)\). In der Zeichenebene (x2x3) bzw. wenn man die x1-Achse nicht berücksichtigit, wird er bei \((3|1)\) eingezeichnet. Bestimme eine Formel für diese Projektion in die Zeichenebene! Begründe, wie sich die Koordinaten 3 und 1 aus den Koordinaten des Punktes ergeben.
Im Schaubild siehst du den Punkt \(P(2|4|2)\). In der Zeichenebene (x2x3) bzw. wenn man die x1-Achse nicht berücksichtigit, wird er bei \((3|1)\) eingezeichnet. Bestimme eine Formel für diese Projektion in die Zeichenebene! Begründe, wie sich die Koordinaten 3 und 1 aus den Koordinaten des Punktes ergeben.
| AFB II - K1 K5 | Quelle Holger Engels |
4 Punkt angeben (1 min)
a) Gib an, in welcher Koordinatenebene der Punkt \(A(2|1|0)\) liegt.
b) Nenne einen Punkt, der auf der \(x_1\)-Achse liegt.
| AFB I - K4 K5 | Quelle Martina Wagner |
5 Spiegelung von Punkten an Koordinatenebenen (6 min) 𝕃
Gib an, welche Koordinaten die Bildpunkte von A, B und C haben, bei einer Spiegelung von
a)\(A(2|4|2)\) an der \(x_1x_2-\)Ebene,
b)\(B(-4|1|-1)\) und \(C(5|-8|0)\) bei Spiegelung b) \(x_1x_3-\)Ebene und an der c) \(x_2x_3-\)Ebene haben.
| AFB I - K5 | Quelle Martin Stern |
6 Museum (7 min) 𝕃
Ein Architekt plant ein modernes Museum.
Im Modell hat das Museum eine rechteckige Grundfläche mit den Eckpunkten \(A_1(0|0|0)\), \(B_1(10|0|0)\), \(C_1(10|5|0)\) und \(D_1(0|5|0)\).
Das Dach hat die vier Eckpunkte: \(A_2(0|0|2)\), \(B_2(10|0|2)\), \(C_2(10|6|2)\) und \(D_2(0|5{,}5|2{,}5)\).
Die von der Grundfläche zum Dach verlaufenden Kanten des Modells verbinden Punkte gleichen Buchstabens, z. B. Ist \(A_1\) mit \(A_2\) verbunden. 1 cm im Modell entspricht 10 m.
Zeichne das Modell in ein geeignetes Koordinatensystem.
| AFB I - K5 | Quelle Abi 2020 Vektorgeometrie mit Hilfsmitteln |
7 Kiste (8 min) 𝕃
Eine Kiste mit rechteckiger Grundseite hat ein Fassungsvolumen von \(144cm^3\). Alle Kanten verlaufen parallel zu den Koordinatenachsen.
Die Darstellung zeigt die Kiste nicht maßstabsgetreu. Eine Längeneinheit entspricht der Länge 1 cm.
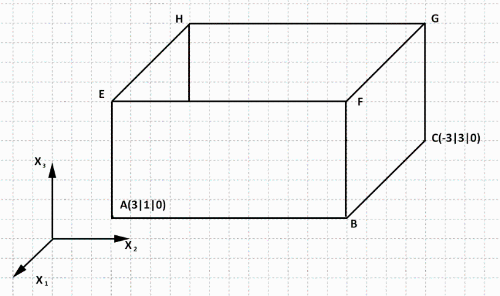
a) Bestimme die Koordinaten der Punkte B und D.
b) Bestimme die Koordinaten der Punkte E und F.
| AFB II - K2 K4 K5 | Quelle kickoff |
8 Polya-Stöpsel (6 min) 𝕃
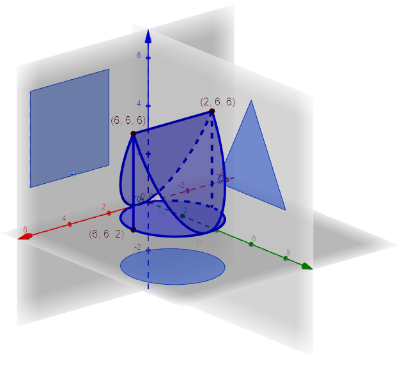 Der Polya-Stöpsel ist ein dreidimensionales Objekt, dessen Projektionen in die Koordinatenebenen ein Dreieck, ein Quadrat und ein Kreis sind. Gib die Koordinaten der Eckpunkte von Dreieck und Quadrat sowie den Mittelpunkt und den Radius des Kreises an.
Der Polya-Stöpsel ist ein dreidimensionales Objekt, dessen Projektionen in die Koordinatenebenen ein Dreieck, ein Quadrat und ein Kreis sind. Gib die Koordinaten der Eckpunkte von Dreieck und Quadrat sowie den Mittelpunkt und den Radius des Kreises an.
| AFB II - K5 | Quelle Holger Engels |
9 Eckpunkte einer Pyramide (11 min) 𝕃
In einem kartesischen Koordinatensystem ist die gerade Pyramide ABCDS gegeben. Die Kantenlänge der quadratischen Grundfläche ist 5, die Höhe der Pyramide 7.
- Gib mögliche Koordinaten der Eckpunkte der Pyramide an.
- Mindestens einer der Eckpunkte soll so verschoben werden, dass sich das Volumen der Pyramide vervierfacht. Dafür gibt es mehrere Möglichkeiten. Gib für zwei dieser Möglichkeiten jeweils die Koordinaten der verschobenen Eckpunkte an und begründe deine Angabe.
| AFB III - K1 K2 K5 | Quelle IQB | #iqb |
Vektoren
10 Vektorbegriff (3 min) 𝕃
Begründe, was ein Vektor ist. Kreuze alle richtigen Aussagen an.
A ☐ Ein Vektor ist eine Pfeilmenge.
B ☐ Ein Vektor wird geschrieben als: \(\vec{v}\)
C ☐ Ein Vektor ist ein Punkt.
D ☐ Geometrisch betrachtet sind alle Pfeile eines Vektors gleichlang.
E ☐ Geometrisch betrachtet sind alle Pfeile eines Vektors gleichgerichtet.
F ☐ Geometrisch betrachtet sind alle Pfeile eines Vektors parallel.
G ☐ Der Ortsvektor eines Punktes ist der Verbindungsvektor vom Ursprung zu diesem Punkt.
H ☐ Pfeile, die zu einem Vektor gehören, können in unterschiedliche Richtungen zeigen.
I ☐ Pfeile, die zu einem Vektor gehören, beginnen immer im Ursprung.
In Anlehnung an: Henrik Horstmann, Aufgaben zu Vektoren,CC BY 4.0
| AFB I - K6 | Quelle Martin Stern |
11 Koordinatendarstellung (2 min) 𝕃
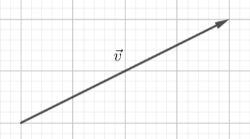 Gib die Koordinatendarstellung des Vektors an.
Gib die Koordinatendarstellung des Vektors an.
Zeichne einen weiteren Repräsentanten und den Gegenvektor daneben.
| AFB I - K4 | Quelle Martin Stern |
12 Zeichnen 2D (3 min) 𝕃
Gegeben sind die Punkte A(-1|-2) und B(3|1). Zeichne den Ortsvektor \(\overrightarrow{OA}\) und den Verbindungsvektor \(\overrightarrow{AB}\) in ein geeignetes Koordinatensystem.
| AFB I - K4 | Quelle Holger Engels |
13 Vektor und Gegenvektor (4 min) 𝕃
Gegeben sind die Punkte \(A(3|5|-8)\) und \(B(-5|1|6)\). Gib den Vektor \(\overrightarrow{AB}\) und \(\overrightarrow{BA}\) an.
| AFB I - K5 | Quelle Martin Stern |
14 Verschiebung (4 min) 𝕃
Das Dreieck ABC mit A(2|-1|2), B(-2|-3|1), C(-2|1|0) soll durch den Vektor \(\vec{v}=\left(\begin{array}{c}2 \\ 4 \\ 2 \end{array}\right)\) verschoben werden. Zeichne das Dreieck zusammen mit seinem Abbild in ein geeignetes Koordinatensystem.
| AFB I - K4 | Quelle Holger Engels |
15 Verschiebung ermitteln (5 min) 𝕃
 Die Koordinaten der Eckpunkte des linken Dreiecks lauten: \(A(4|-3|3)\text{, }B(4|1|3)\text{ und }C(2|4|5)\)
Die Koordinaten der Eckpunkte des linken Dreiecks lauten: \(A(4|-3|3)\text{, }B(4|1|3)\text{ und }C(2|4|5)\)
Vom Punkt A' ist bekannt, dass er in der x2x3-Ebene liegt. Bestimme den Verschiebungsvektor und ermittle die Koordinaten von B' und C'
| AFB II - K5 | Quelle Holger Engels |
16 Pyramide (11 min) 𝕃
Betrachtet wird die Pyramide \(ABCS\). Ihre Grundfläche ist das rechtwinklige Dreieck \(ABC\); die Hypotenuse \(\overline{AB}\) ist 5 cm lang, die Kathete \(\overline{AC}\) 4 cm. Die Kante \(\overline{CS}\) steht senkrecht zur Grundfläche und hat eine Länge von 7 cm.
- Berechne das Volumen der Pyramide.
- Die Pyramide soll in einem Koordinatensystem dargestellt werden, in dem eine Längeneinheit 1 cm entspricht. Gib mögliche Koordinaten der Eckpunkte der Pyramide an!
| AFB II - K2 K6 | Quelle IQB 2020 Lineare Algebra gAN Teil A |
17 Körpernetz (5 min) 𝕋 𝕃
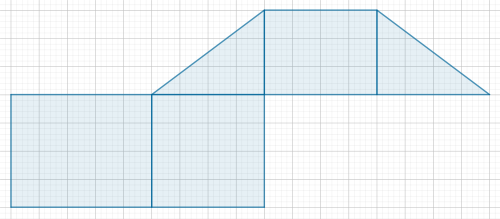 Nenne den geometrischen Körper, der durch Zusammenfalten das Netzes entsteht. Zeichne den Körper in ein 3D-Koordinatensystem, wobei eine Dreiecksfläche in der x1x2-Ebene zu liegen kommen soll.
Nenne den geometrischen Körper, der durch Zusammenfalten das Netzes entsteht. Zeichne den Körper in ein 3D-Koordinatensystem, wobei eine Dreiecksfläche in der x1x2-Ebene zu liegen kommen soll.
| AFB II - K4 | Quelle Holger Engels |
Inhalt für Lehrende (Anmeldung erforderlich)
