BPE 7.2 Addition, Skalare Multiplikation, Betrag, Abstand, Strecke
K5 Ich kann elementare Rechenoperationen für Vektoren verwenden
K4 Ich kann elementare Rechenoperationen für Vektoren geometrisch deuten
K5 Ich kann den Betrag eines Vektors berechnen
K6 K5 Ich kann den Betrag eines Vektors als seine Länge interpretieren
K5 Ich kann Vektoren zur Bestimmung von Teilpunkten einer Strecke verwenden
Vektoren
1 Vektor (5 min) 𝕋 𝕃
Der Vektor \(\vec{a}= \left(\begin{array}{c} a_1 \\ a_2 \end{array}\right)\) verläuft parallel zur zweiten Winkelhalbierenden.
Zusätzlich soll gelten: \(\left(\begin{array}{c} 3 \\ 1 \end{array}\right) + \vec{a} = \left(\begin{array}{c} 0,5 \\ d \end{array}\right)\).
Bestimme den Wert von d.
| AFB I - K5 | Quelle Daniel Stocker |
2 Vektoraddition (5 min)
Gegeben sind die Punkte \(A(3|1|5)\), \(B(5|2|4)\) und \(C(8|7|1)\).
Berechne die Koordinaten von einem Punkt \(D(d_1|d_2|d_3)\), wobei gilt: \(\overrightarrow{AB}-\overrightarrow{CA}+\overrightarrow{BC}-\overrightarrow{DA}=\overrightarrow{o}\)
| AFB I - K5 | Quelle Daniel Stocker |
3 3D-Koordinatensystem (k.A.)
In einem Koordinatensystem ist ein gerader Zylinder mit dem Radius 5 und der Höhe 10 gegeben, dessen Grundfläche in der \(x_1x_2\)-Ebene liegt. \( M(8|5|10)\) ist der Mittelpunkt der Deckfläche.
- Weise nach, dass der Punkt \(P(5|1|0) \) auf dem Rand der Grundfläche des Zylinders liegt.
- Unter allen Punkten auf dem Rand der Deckfläche hat der Punkt \( S \) den kleinsten Abstand von \( P \), der Punkt \( T \) den größten. Gib die Koordinaten von \( S \) an und bestimme die Koordinaten von \( T \).
| AFB II - K1 K2 K5 | Quelle IQB | #iqb |
4 Dreieck Koordinaten (6 min)
Gegeben sind die Punkte \( A(5|0|a)\) und \(B(2|4|5)\). Der Koordinatenursprung wird mit \(O\) bezeichnet.
- Bestimme denjenigen Wert von \( a\), für den \(A\) und \(B\) den Abstand 5 haben.
- Ermittle denjenigen Wert von \( a\), für den das Dreieck \(OAB\) im Punkt \(B\) rechtwinklig ist.
| AFB II - K2 K5 | Quelle IQB | #iqb |
5 Vektoraddition (5 min)
Gegeben sind die Punkte \(A(3|1|5)\), \(B(5|2|4)\) und \(C(8|7|1)\).
Berechne die Koordinaten von einem Punkt \(D(d_1|d_2|d_3)\), wobei gilt: \(\overrightarrow{AB}-\overrightarrow{CA}+\overrightarrow{BC}-\overrightarrow{DA}=\overrightarrow{o}\)
| AFB I - K5 | Quelle Daniel Stocker |
6 Vektoren Sechseck (k.A.) 𝕃
Im abgebildeten Sechseck \(ABCDEF\) sind jeweils zwei Seiten parallel zueinander.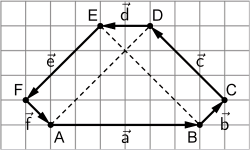
a) Stelle die Vektoren \(\Vec{x} \) und \(\Vec{y} \) jeweils mithilfe der Eckpunkte des Sechsecks dar.
b) Stelle den Vektor \(\overrightarrow{FB} \) mithilfe der Vektoren \(\Vec{a}, \Vec{b}, \Vec{c}, \Vec{d}, \Vec{e} \) und \(\Vec{f} \) dar.
c) Der Punkt \(A\) hat in einem kartesischen Koordinatensystem die Koordinaten \(x_1 = 6, x_2 = 2 \) und \(x_3=-4\) Der Mittelpunkt der Strecke \(\overline{AB} \) wird mit \(M \) bezeichnet. Der Punkt \(K(2|0|8)\) ist der Mittelpunkt der Strecke \( \overline{AM} \). Ermittle die Koordinaten von \(B\).
| AFB II - K2 K4 K5 | Quelle IQB | #iqb |
7 Nachweis Dreieck (k.A.) 𝕋 𝕃
In einem kartesischen Koordinatensystem sind die Punkte \(A(1|2|5)\), \(B(2|7|8)\) und \(C(-3|2|4)\) gegeben.
- Weise nach, dass \(A, B\) und \(C\) Eckpunkte eines Dreiecks sind.
- Für jede reelle Zahl \(a\) ist ein Punkt \( D_a(a|2+a\sqrt{2}|5+\sqrt{2}) \) gegeben. Bestimme alle Werte von \(a\), für die die Strecke von \( A\) nach \(D_a\) die Länge 2 hat.
| AFB III - K1 K2 K5 | Quelle IQB | #iqb |
