BPE 7.3 Skalarprodukt, Winkel und Orthogonalität
Kompetenzen
K6 Ich kann die Bedeutung des Skalarprodukts in der Geometrie erläutern
K5 Ich kann Winkel zwischen zwei Vektoren bestimmen
K5 K6 Ich kann geometrische Objekte in Ebene und Raum untersuchen
1 Winkel berechnen (3 min) 𝕋 𝕃
Berechne jeweils den Winkel zwischen den beiden Vektoren:
a) \(\vec a = \left(\begin{array}{c} 7 \\ 5 \\ -3\end{array}\right), \vec b = \left(\begin{array}{c} -1 \\ 2 \\ -2\end{array}\right)\)
b) \(\vec a = \left(\begin{array}{c} 7 \\ 5 \\ -3\end{array}\right), \vec c = \left(\begin{array}{c} 1,5 \\ 2,1 \\ 7\end{array}\right)\)
| AFB I - K5 | Quelle Kim Fujan, Daniel Stocker |
2 Orthogonalen Vektor finden (3 min) 𝕃
Bestimme a, sodass der Vektor \(\vec u = \left(\begin{array}{c} 4 \\ 5 \\ 2\end{array}\right)\) zu dem Vektor \(\vec v = \left(\begin{array}{c} \frac{2}{3} \\ a \\ 1\end{array}\right)\) orthogonal ist.
| AFB I - K5 | Quelle Kim Fujan, Daniel Stocker |
3 Flächenberechnung Dreieck (5 min) 𝕋 𝕃
Berechne den Flächeninhalt des Dreiecks, das durch die Punkte A(2|-1|4), B(0|9|-3), C(-2|5|1) festgelegt wird.
| AFB I - K5 | Quelle Kim Fujan, Daniel Stocker |
4 Skalarprodukt null (2 min) 𝕃
Gegeben ist der Vektor
Gib einen Vektor an, der orthogonal zu diesem ist!
| AFB II - K5 K2 | Quelle Holger Engels |
5 Orthogonalität transitiv (3 min)
Von drei Vekoren im Raum ist folgendes bekannt. Vektor \(\vec b\) steht auf \(\vec a\) senkrecht und \(\vec c\) auf \(\vec b\). Kann man daraus folgern, dass auch \(\vec c\) auf \(\vec a\) senkrecht stehen muss?
Begründe deine Antwort!
| AFB II - K1 K2 | Quelle Holger Engels |
6 Skalarprodukt negativ (5 min) 𝕋 𝕃
Gib zwei Vektoren an, deren Skalarprodukt negativ ist. Prüfe, ob der Winkel zwischen den Vektoren größer 90° ist. Ist das immer so? Begründe!
| AFB III - K1 K2 K5 | Quelle Holger Engels |
7 Drachen begründen (5 min) 𝕋 𝕃
Begründe, dass es sich bei dem gegebenen Viereck um einen Drachen handelt: A(8,5|5|-3,5), B(4|5|-2), C(-3,5|8|2,5), D(5|7|-1).
| AFB III - K1 K5 K6 | Quelle Kim Fujan, Daniel Stocker |
8 Quadrat begründen (4 min) 𝕋 𝕃
Begründe, dass es sich bei dem gegebenen Viereck um ein Quadrat handelt: A(5|-1|3), B(1|1|-1), C(-1|5|3), D(3|3|7).
| AFB II - K1 K5 K6 | Quelle Kim Fujan, Daniel Stocker |
9 Pfahlbauten (9 min) 𝕋 𝕃
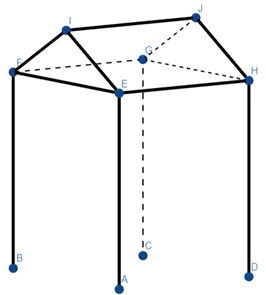
Es soll eine Rekonstruktion eines Hauses der Pfahlbauten am Bodensee gebaut werden. Die vertikalen Pfosten haben eine Gesamthöhe von 7,5m. Das Dach hat die Form eines Dreieckprismas (siehe Nebenstehende Abbildung). Die Dicke der Bauteile des Hauses soll vernachlässigt werden. Die Eckpunkte haben die Koordinaten A(-2| 1|w), B,C(5|-5|w), D, E, F(5|1|3), G,H,I(1,5|1|5),J mit \(w \in \mathbb{R}\). Die x1 x2- Ebene bildet die Wasseroberfläche. 1m in der Wirklichkeit entspricht einer Längeneinheit im Koordinatensystem.
a) Wieviel Meter der Pfosten befinden sich oberhalb des Wassers?
b) Gebe die Koordinaten der Punkte G,H und J an.
c) Berechne die Dachfläche.
d) Berechne den Neigungswinkel des Daches.
| AFB II - K3 K5 K6 | Quelle Kim Fujan, Daniel Stocker |
10 Punktbestimmung durch Skalarprodukt (6 min) 𝕃
Gegeben sind die Punkte A(2|-3|1) und B(2|3|1).
- Begründe, dass die Gerade durch \(A \) und \(B\) parallel zur y-Achse verläuft.
- Der Punkt \(C\) liegt auf der y-Achse. Die Gerade durch \(A\) und \(C\) steht senkrecht zur Gerade durch \(B\) und \( C\). Bestimme die Koordinaten aller Punkte, die die beschriebenen Eigenschaften des Punkts \(C\) haben.
| AFB II - K1 K2 K4 K5 K6 | Quelle IQB | #iqb |
